贝叶斯分类器

核心思想

贝叶斯分类器是一种基于贝叶斯定理的统计分类方法。在给定数据的情况下，它使用概率模型来预测数据点的类别。贝叶斯分类器的核心思想是，对于给定的样本，我们可以计算它属于每个类别的概率，并将样本分配给概率最大的类别。

贝叶斯公式： \[ P(A | B) = \frac{P(B | A) P(A)}{P(B)} \]

先验概率（Prior Probability）：指在没有额外信息的情况下，一个事件发生的概率。
后验概率（Posterior Probability）：给定某些证据后，时间发生的概率。
似然性（Likelihood）：给定假设为真时观察到证据的概率。

使用后验概率来进行分类的分类器称之为贝叶斯分类器（Bayes Classifier）。

数学表示

我们以二分类问题为例，假设在数据集 \(S\) 中的数据有两个类 \(A\) 和 \(B\) ，则贝叶斯分类器一般用优势比（Odds Ratio）来描述某个数据点的所属类别： \[ \frac{P(y = A|x)}{P(y = B|x)} \]

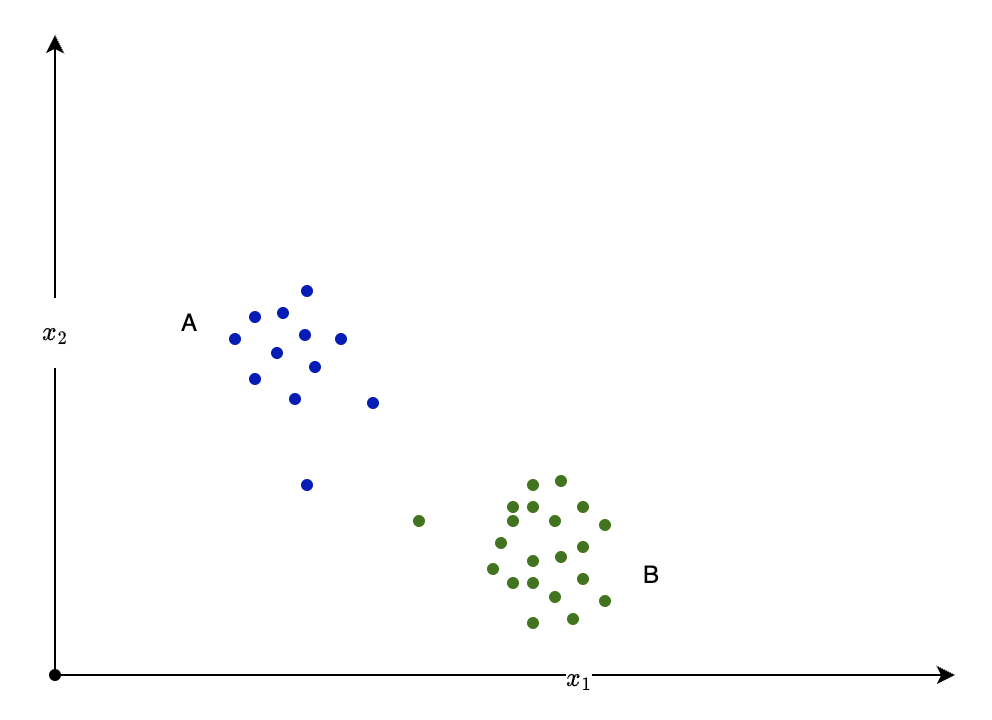
若上式子大于 1，即 \(P(y = A | x) > P(y = B | x)\)，则认为数据点的特征向量为 \(x\) 的情况下，其属于 \(A\) 类的概率更大，反之则认为其属于 \(B\) 类的概率更大。

根据贝叶斯公式，上式可以表示为： \[ \frac{P(x | y = A) P(y = A)}{P(x | y = B) P(y = B)} \] 其中 \(P(y = A)\) 和 \(P(y = B)\) 由两个类别在数据集中的占比决定，而 \(P(x | y = A)\) 和 \(P(x | y = B)\) 则由两个类别中数据的分布相关。

判别分析

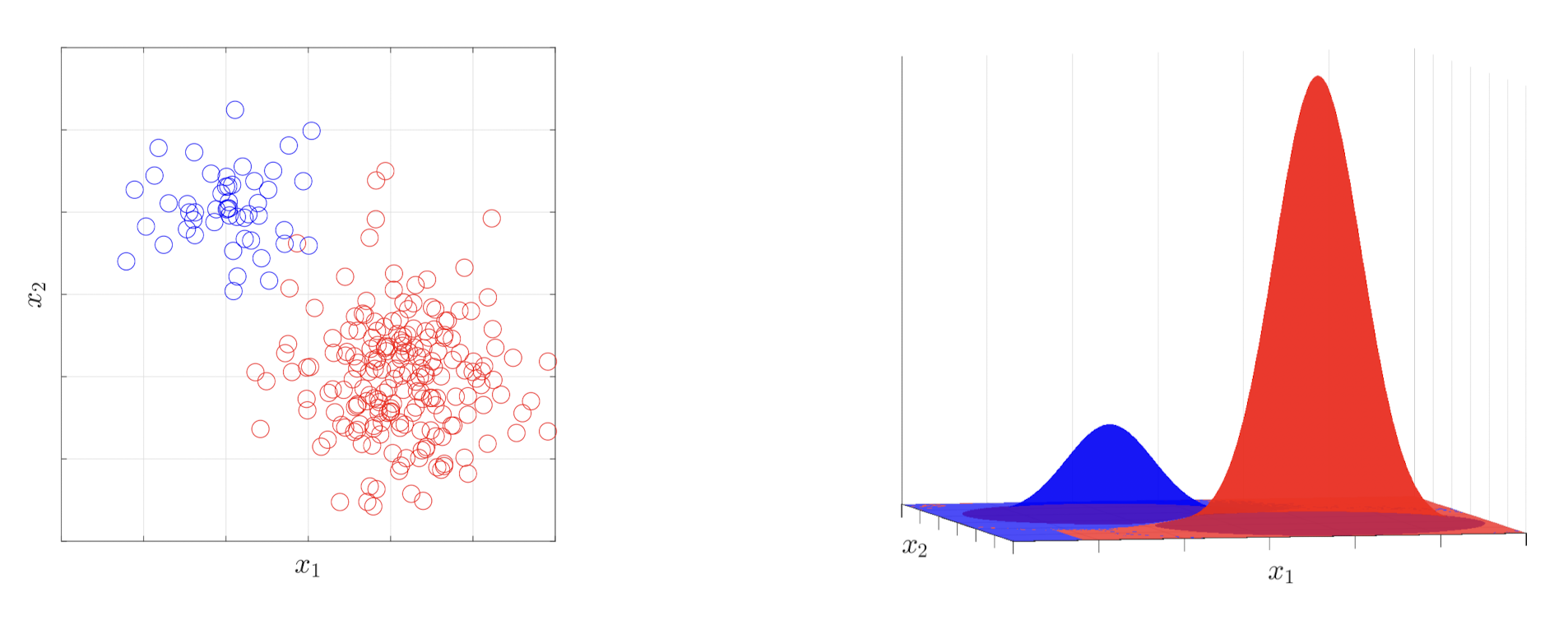
判别分析（Discriminant Analysis）是机器学习和统计学中的一种技术，用于将一组观测值分类到预定义的类别中。该方法假设不同的类别通过不同的高斯分布（Guassian Distribution）生成数据。

\[ p(x | y = A) = \frac{1}{(2 \pi) ^ {\frac{d}{2}} {|\Sigma_A|} ^ \frac{1}{2}} exp(-\frac{1}{2}(x - \mu_A) ^ T \Sigma_A^{-1} (x - \mu_A)) \]

\[ p(x | y = B) = \frac{1}{(2 \pi) ^ {\frac{d}{2}} {|\Sigma_B|} ^ \frac{1}{2}} exp(-\frac{1}{2}(x - \mu_B) ^ T \Sigma_B^{-1} (x - \mu_B)) \]

主要类型的判别分析包括：

线性判别分析（Linear Discrinant Analysis，LDA）：这种方法假设不同类别具有相同的协方差矩阵。它找到一个特征的线性组合，这个组合能够表征或者区分两个或多个类别。目的是在类别之间找到一个线性边界。
二次判别分析（Quadratic Discrinant Analysis，QDA）：与 LDA 不同，QDA 假设每个类别都有自己的协方差矩阵。它在分类上更加灵活，因为它可以创建二次边界，因此得名。

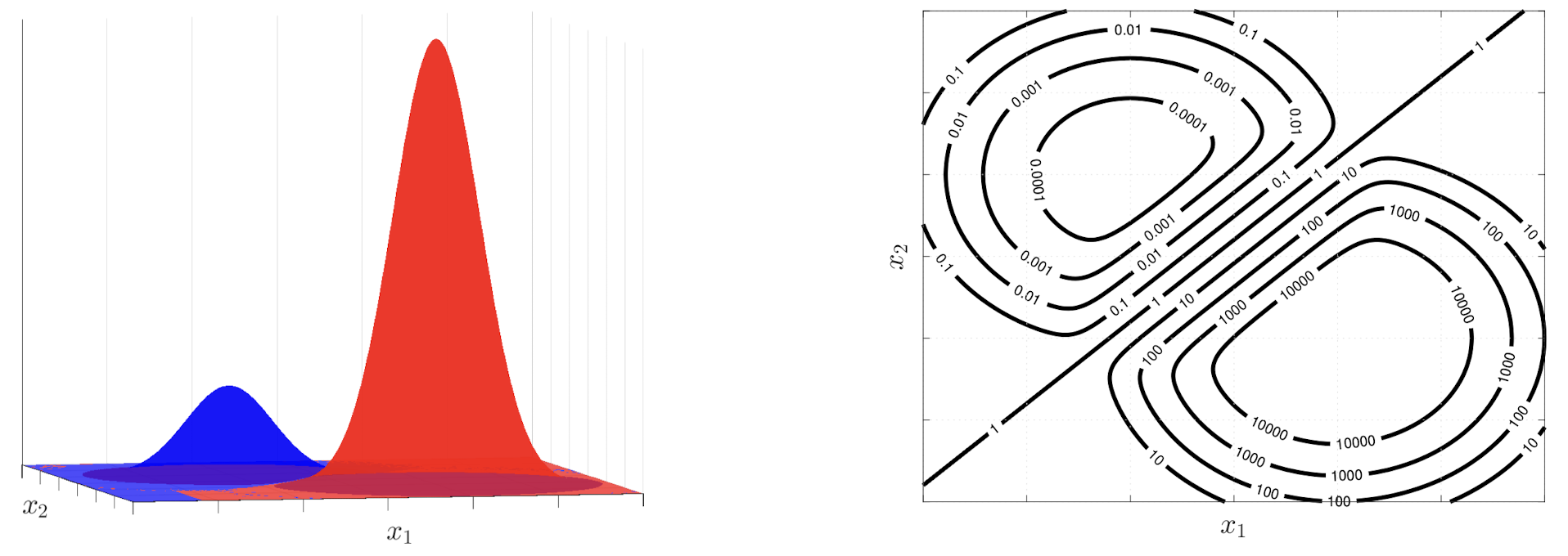
通常而言，两个类别的协方差矩阵相等或者十分接近，例如其差值的矩阵二范数 \(||\Sigma_A - \Sigma_B || ^ 2\) 是一个很小的值，我们就可以认为数据集的判别分析类型为 LDA。

考虑错误分类成本

在机器学习和统计分类问题中，错误分类成本（Misclassification Costs）指的是将一个实例错误分类为另一个类别时所产生的代价或损失。在某些情况下，不同类型的错误可能会导致不同程度的负面影响。例如，在医疗诊断中，将患有疾病的病人错误地判定为健康（漏诊）通常比将健康的病人错误判定为患病（误诊）带来更严重的后果。

错误分类成本可以是不对称的，意味着对于不同的错误分类，成本可以不一样。在设计分类器时，我们通常希望最小化总体的错误分类成本，而不仅仅是错误分类的数量。

考虑错误分类成本的贝叶斯分类器（也称为成本敏感的贝叶斯分类器）是一种在决策过程中考虑到不同类型错误分类所带来成本的分类器。这种分类器不仅仅追求最大化整体的准确率，而是尝试最小化总的期望分类成本。

以上文提及的二分类为例，我们定义成本矩阵（Costs Matrix）： \[ C = \begin{bmatrix} C(A | A) & C(A | B) \\ C(B | A) & C(B | B) \end{bmatrix} \] 在成本矩阵中 \(C(I | J)\) 表示将标签为 \(J\) 类的数据识别为 \(I\) 类需要付出的成本。

对于一个新的实例 \(x\) ，我们可以计算出其属于每个类别的期望成本： \[ EC(y = A | x) = P(y = A | x)C(A | A) + P(y = B | x) C(A | B) \]

\[ EC(y = B | x) = P(y = B | x)C(B | B) + P(y = A | x)C(B | A) \]

最后我们只需要选择期望成本最小的类别即可，我们一般认为 \(C(A | A) = C(B | B) = 0\)，因为通常情况下正确识别不需要花费额外的成本。

因此考虑错误分类成本的优势比可以表示如下： \[ \frac{P(y = A | x)C(B | A)}{P(y = B | x)C(A | B)} \] 即如果满足 \(\frac{P(y = A | x)}{P(y = B |x)} > T\ (T = \frac{C(A | B)}{C(B | A)})\) ，则考虑将样本 \(x\) 划分为 A 类更合适。\(T\) 在这里就是分类器的阈值，不同的 \(T\) 会有不同的分类边界。

分类器的评估

混淆矩阵

混淆矩阵（Confusion Matrix）是一种特定的表格用于可视化算法性能，尤其是在监督学习中对分类问题的性能评估。它展示了实际类别与模型预测类别之间的关系，以此来揭示模型在各个类别上的错误类型。

对于一个二分类问题，混淆矩阵包含四个部分：

真正例（True Positives, TP）：模型正确预测为正类的数量。
假正例（False Positives, FP）：模型错误预测为正类的数量。
真负例（True Negatives, TN）：模型正确预测为负类的数量。
假负例（False Negatives, FN）：模型错误预测为负类的数量。

混淆矩阵通常如下所示：

\[ \begin{array}{cc} & \text{预测正类} & \text{预测负类} \\ \text{实际正类} & TP & FN \\ \text{实际负类} & FP & TN \\ \end{array} \] 这个矩阵使我们能够快速计算出几个重要的性能指标，如：

准确率（Accuracy）：所有正确分类的观测值占总观测值的比例，计算公式为 \((TP + TN) / (TP + TN + FP + FN)\)。
精确率（Precision）：正确预测为正类的观测值占预测为正类的比例，计算公式为 \(TP / (TP + FP)\)。
召回率（Recall）或灵敏度（Sensitivity）：正确预测为正类的观测值占实际正类的比例，计算公式为 \(TP / (TP + FN)\)。
特异性（Specificity）：正确预测为负类的观测值占实际负类的比例，计算公式为 \(TN / (TN + FP)\)。

解决一个分类问题，实际上即使要找到一个分类边界，可以最大化敏感度和特异性。

ROC 平面与 AUC 指标

ROC（接收者操作特征）平面是用来评估二分类系统性能的图形化工具。它通过绘制真正例率（True Positive Rate, TPR）对假正例率（False Positive Rate, FPR）来展示分类器的性能。

在 ROC 平面中：

真正例率（TPR），也就是召回率（Recall）或灵敏度（Sensitivity），是指正确识别为正例的样本占所有实际正例的比例。计算公式为：\(\text{TPR} = \frac{TP}{TP + FN}\)。
假正例率（FPR），是指错误识别为正例的样本占所有实际负例的比例。计算公式为：\(\text{FPR} = \frac{FP}{TN + FN}\) ，即 \(1 - \text{specificity}\)。

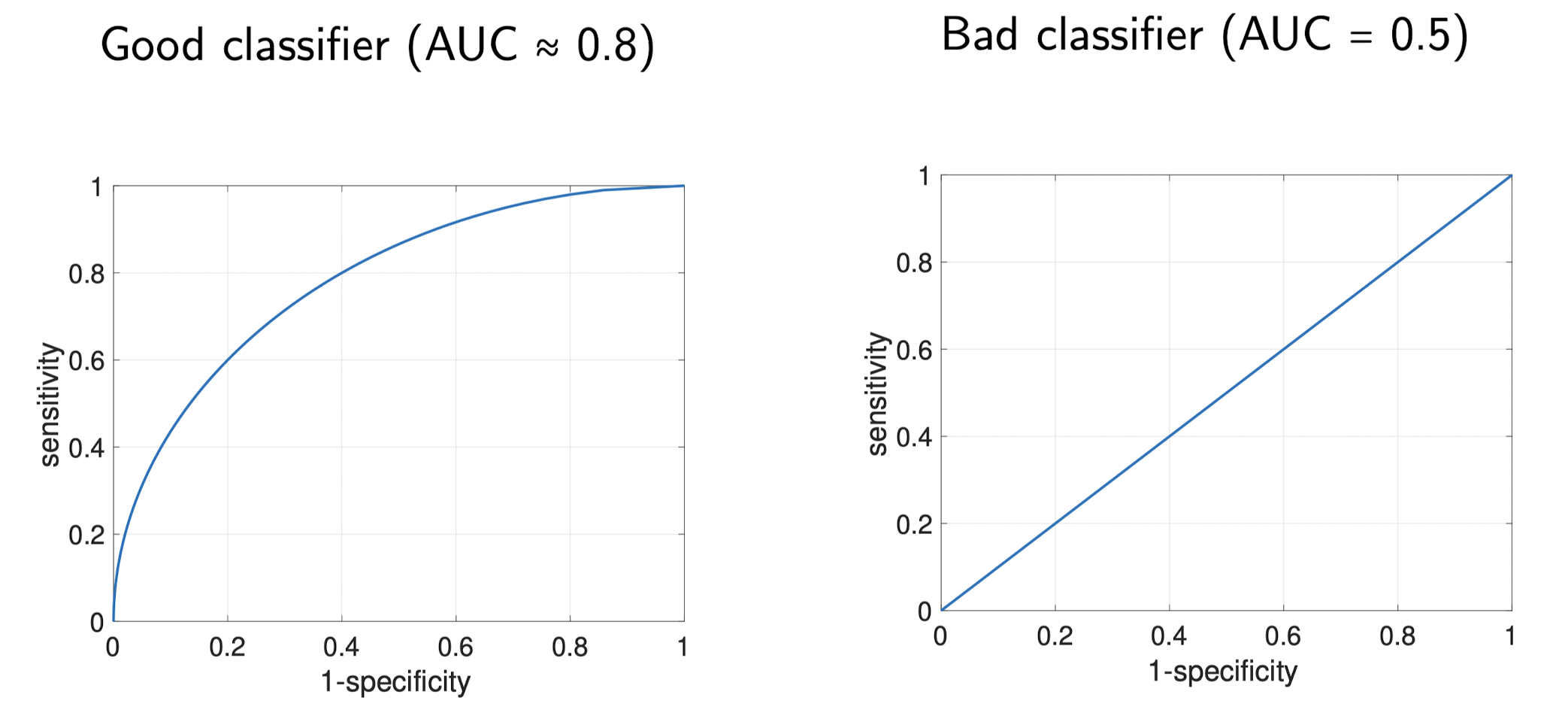
在 ROC 曲线上，每个点代表对应于某个决策阈值的（FPR，TPR）对。曲线下面积（Area Under the Curve，AUC）用来量化分类器的总体性能：AUC值为 1 表示完美分类器，AUC 值为 0.5 表示无效分类器，即其性能不如随机猜测。

ROC平面上的主要特点包括：