神经网络介绍
从感知机到神经网络
感知机(perceptron) 是美国学者 Frank Rosenblatt 在
1957 年提出的概念。
感知机可以理解成某个节点,接受一个或者多个信号,输出一个信号。在数字电路中常讨论的各种逻辑门,都可以看成感知机。
以下就是一个简单的感知机的例子:
\[
\begin{equation}
y =
\begin{cases}
0 & (w_1 x_1 + w_2 x_2 \leq 0) \\
1 & (w_1 x_1 + w_2 x_2 > 0)
\end{cases}
\end{equation}
\] 而神经网络就是由很多层复杂的感知机组合而成的。
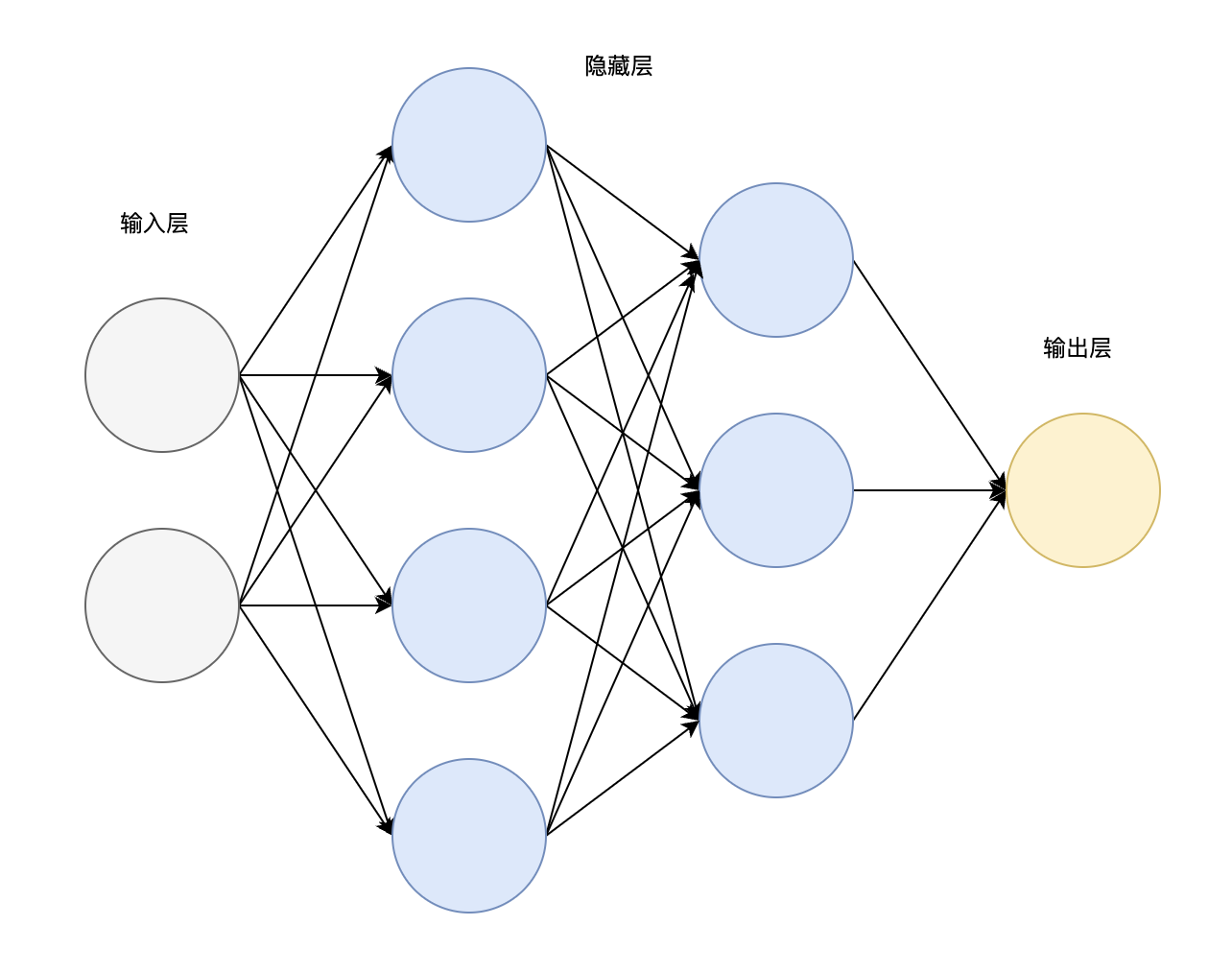
一般而言,神经网络由三个主要部分组成:
输入层(Input Layer) 隐藏层(Hidden Layer) 输出层(Output Layer)
一般而言,一个 \(k\) 层神经网络有
\(k - 1\) 个隐藏层。
Affine 函数
Affine
函数即对上一层节点传输数值作仿射变换,一般是所有数值的线性组合加上一个常量。
\[
y_i = \sum_{k = 1} ^ m w_{k, i} x_k + b_i
\] 矩阵乘法表示为: \[
y = X W + b
\]
激活函数
激活函数(activation
function) 就是将输入信号转化为输出信号的函数。激活函数的作用在于决定如何来激活输入信号的总和。
下面是几种常见的激活函数:
阶跃函数
\[
\begin{equation}
h(x) =
\begin{cases}
1 & (x > 0) \\
0 & (x \leq 0)
\end{cases}
\end{equation}
\]
跃阶函数非常简单,输入值大于 0 时输出 1,否则输出 0。
代码实现:
1 2 3 def step_function (x ):return (x > 0 ).astype(np.int )
Sigmoid 函数
\[
h(x) = \frac{1}{1 + exp(-x)}
\]
Sigmoid 函数可以将全体实数平滑映射到 \((0,
1)\) ,在神经网络中被广泛使用。
代码实现:
1 2 3 def sigmoid (x ):return 1 / (1 + np.exp(-x))
以上提及的两种激活函数都属于非线性函数,神经网络的激活函数必须使用非线性函数,如果激活函数都是线性的,那么不论神经网络有多少层,最后的激活值都是输入值的线性组合,无法发挥神经网络的作用。
ReLU 函数
\[
\begin{equation}
h(x) =
\begin{cases}
x & (x > 0) \\
0 & (x \leq 0)
\end{cases}
\end{equation}
\]
ReLU(Rectified Linear
Unit) 函数,即线性修正单元函数,当输入值大于 0
时输出输入值本身,否则输出 0。
代码实现:
1 2 3 def relu (x ):return np.maximum(0 , x)
输出层设计
神经网络可以用在预测问题和分类问题上,根据我们要解决的问题可以改变输出层的激活函数。
一般而言,预测问题用恒等函数 ,分类问题用
Softmax 函数 。
恒等函数
恒等函数会原样输出信息,不加以任何改动。一般用于像回归这样的预测问题上。
Softmax 函数
\[
y_k = \frac{exp(x_k)}{\sum_{i = 1}^n exp(x_i)}
\]
不难发现,Softmax 函数处理后的向量元素和为
1,由于指数函数爆炸式增长的性质,不同元素的差异会被放大。一般用于分类问题上,使用
Softmax
函数激活输出节点后某个节点的值越大,说明输入输入该类的可能性越大。
代码实现:
1 2 3 4 def softmax (x ):return exp_x / np.sum (exp_x)
神经网络代码实现
综上,以下给出一个简单的二层神经网络的实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class TwoLayersNetWork :def __init__ (self, input_size, hidden_size, output_size, init_std = 0.01 ):'W1' ] = init_std * np.random.randn(input_size, hidden_size)'b1' ] = init_std * np.random.randn(hidden_size)'W2' ] = init_std * np.random.randn(hidden_size, output_size)'b2' ] = init_std * np.random.randn(output_size)def forward (self, x ):'W1' ]) + self.params['b1' ]'W2' ]) + self.params['b2' ]return x2
神经网络的学习
神经网络的特征就是可以从数据中学习。所谓从数据中学习,就是根据数据自动决定权重参数的值。
机器学习中,一般将数据分为训练数据和测试数据两部分来进行学习和实验,训练数据也称为监督数据,用来评价模型的泛化能力 。
损失函数
损失函数(Loss
Function) 是用来评判神经网络性能的指标,损失函数可以使用任意函数,但一般用均方误差和交叉熵误差等。
均方误差
均方误差(Mean Squared
Error) 是非常著名的损失函数,其表达式如下: \[
E = \frac{1}{2}\sum_{k = 1} ^ m (y_k - t_k) ^ 2
\] 这里 \(y_k\) 和 \(t_k\)
分别表示神经网络的输出以及正确数据,\(m\) 表示数据的维度。
代码实现:
1 2 3 def mean_squared_error (y, t ):return 1 / 2 * np.sum ((y - t) ** 2 )
交叉熵误差
除了均方误差之外,交叉熵误差(Cross Entropy
Error) 也经常被用作损失函数。交叉熵误差如下式所示: \[
E = -\sum_{k = 1} ^ m t_k\ ln\ y_k
\] 这里 \(y_k\) 和 \(t_k\)
分别表示神经网络的输出以及正确解标签,\(m\) 表示数据的维度。对于 \(t_k\) 而言,只有正确索引的值为 1,其余都为
0。交叉熵误差一般用作分类问题的损失函数。
代码实现:
1 2 3 4 def cross_entropy_error (y, t ):1e-7 return -np.sum (t * np.log(y + delta))
这里 delta 是一个微小量,防止出现 log(0)
的情况发生。
Mini-batch 学习
机器学习使用训练数据进行学习,其目标就是找出参数使得损失函数的值尽可能地小。因此,计算损失函数时必须把所有的训练数据作为对象。
假设有 \(N\)
个数据数据,那么我们就要求所有训练的损失函数的平均值: \[
E = \frac{1}{N} \sum_{i = 1} ^ N loss(y ^ {(i)}, t ^ {(i)})
\] 但如果数据量过大,会导致每轮学习的时间开销过大。所以我们考虑
mini-batch
学习 ,即每次从所有数据集中随机选取批量数据进行学习,每次计算该批次的数据的损失函数的平均值即可。
在具体的代码实现中,我们可以使用 NumPy 中的
np.random.choice() 来随机选取下标。
1 2 3 batch_mask = np.random.choice(train_size, batch_size)
np.random.choice(train_size, batch_size) 返回一个长度为
batch_size ,数据取值范围为 [0, train_size)
的随机正整数数组。
梯度下降法
机器学习的主要任务是在学习时寻找能使损失函数值最小的最优参数。一般而言,损失函数很复杂,参数空间庞大,很难用常规方式求解最小值。
这里我们给出梯度下降法(Gradient Descent
Method) :
从数学的角度出发,函数的梯度的方向代表函数增加最快的方向,其反方向就是函数减小的最快方向,极值点梯度为
0,所以我们可以在每一轮迭代中让参数往梯度方向减小,从而找到极小值点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def numerical_gradient (f, x ):''' 数值法求解梯度下降法 ''' 1e-5 for idx, val in np.ndenumerate(x):2 * delta)return grads
每轮迭代的数学表示如下: \[
x_i := x_i - \eta \frac{\partial f}{\partial x_i}
\] 其中,\(\eta\)
称为学习率(Learning
Rate) ,学习率决定在一次学习中,在多大程度更新参数。
如果我们采用 mini-batch
学习法每次随机选取一批次数据量,并对其损失函数平均值采用梯度下降法,这样的梯度下降我们就称为随机梯度下降(Stochastic
Gradient Descent) ,简称 SGD 。
误差反向传播法
数值法求解梯度是严格按照偏导数的定义来的,这样求解固然正确,但对于参数很大的情况下效率过低。其实有一种高效的梯度求解方法,就是误差反向传播法。
计算图
书上花了很多篇幅去讲解什么是计算图以及起作用,笔者认为计算图就是将求导的链式法则进行了一个可视化。
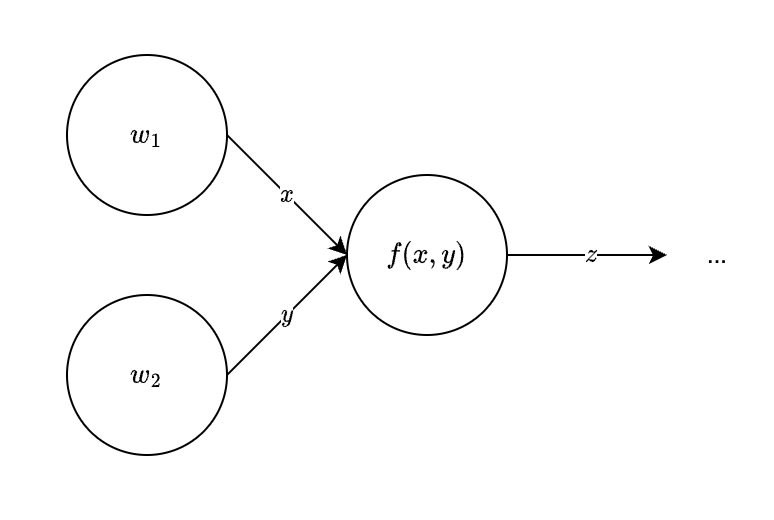
计算图就是通过节点和箭头表示计算过程,如下图:
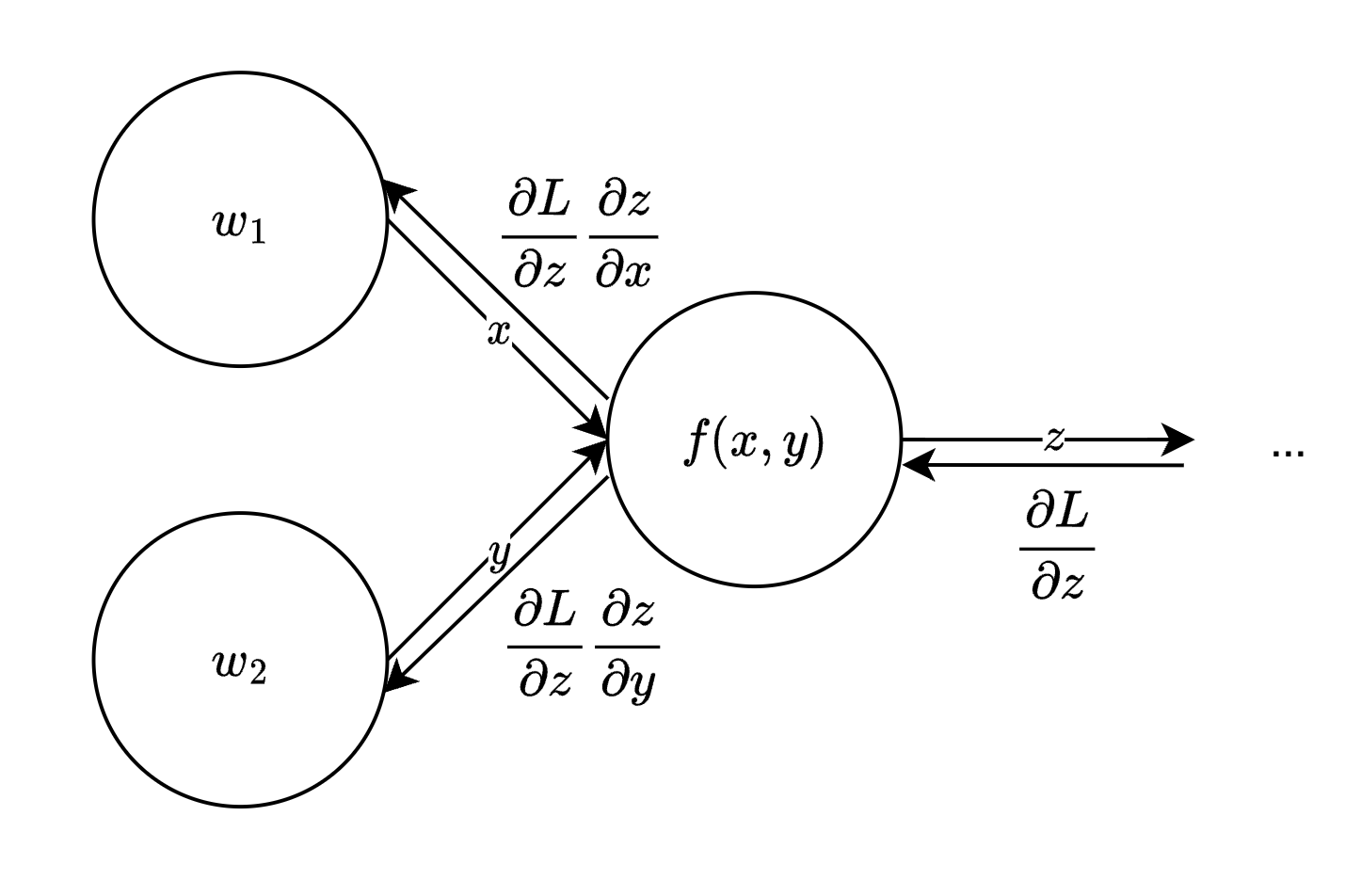
链式法则和反向传播
以上面的图为例,假设我们知道了 \(\frac{\partial L}{\partial z}\)
,根据链式法则可知: \[
\begin{array}{}
\frac{\partial L}{\partial x} = \frac{\partial L}{\partial z}
\frac{\partial z}{\partial x} \\
\frac{\partial L}{\partial y} = \frac{\partial L}{\partial z}
\frac{\partial z}{\partial y}
\end{array}
\]
不难发现,对于一个计算图而言,其数值是正向传播的,而其导数则是反向传播的。
而神经网络不就恰好是一个这样层层传递的计算图吗?
所以我们可以利用链式法则的性质快速计算梯度。
各种层的实现
下面给出各种层的反向传播的实现。
ReLU 层
通过 ReLU 激活函数的表达式,不难得出: \[
\begin{equation}
\frac{\partial y}{\partial x} =
\begin{cases}
1 & (x > 0) \\
0 & (x \leq 0)
\end{cases}
\end{equation}
\] 代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Relu :def __init__ (self ):None def forward (self, x ):0 )0 return outdef backward (self, dout ):0 return dx
Sigmoid 层
同理,我们对原式求导: \[
\begin{array}{}
y = \frac{1}{1 + exp(-x)} \\
\frac{\partial y}{\partial x} = \frac{exp(x)}{(exp(x) + 1) ^ 2} = y (1 -
y)
\end{array}
\] 代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Sigmoid :def __init__ (self ):None def forward (self, x ):return outdef backward (self, dout ):1.0 - self.out) * self.outreturn dx
Affine 层
\[
Y = XW + b
\]
这里涉及到矩阵求导,采用分子布局,若已知 \(\frac{\partial L}{\partial
y}\) ,根据链式求导法则,有: \[
\frac{\partial L}{\partial w_{i, j}} = \sum_k \frac{\partial L}{\partial
y_{k, j}} \frac{\partial y_{k, j}}{\partial w_{i, j}}
\] 代入: \[
y_{k, j} = \sum_{t} w_{t, j} x_{k, t} + b_j
\] 可得: \[
\frac{\partial L}{\partial w_{i, j}} = \sum_k \frac{\partial L}{\partial
y_{k, j}} x_{k, i}
\]
\[
\implies \frac{\partial L}{\partial W} = X ^ T \frac{\partial
L}{\partial Y}
\]
同理,有:\(\frac{\partial L}{\partial X} =
\frac{\partial L}{\partial Y} W ^ T\)
而对于 \(b\)
而言,我们采取同样的方法: \[
\frac{\partial L}{\partial b_i} = \sum_k \frac{\partial L}{\partial
y_{k, i}} \frac{\partial y_{k, i}}{\partial b_i} = \sum_k \frac{\partial
L}{\partial y_{k, i}}
\] 这说明 \(\frac{\partial L}{\partial
b}\) 就等于 \(\frac{\partial
L}{\partial Y}\) 沿列求和。
基于以上的数学证明,我们不难写出 Affine 层的代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Affine :def __init__ (self, W, b ):None None None def forward (self, x ):if x.ndim == 1 :1 , x.size))else :return outdef backward (self, dout ):if dout.ndim == 1 :1 , dout.size))sum (dout, axis = 0 )return dx
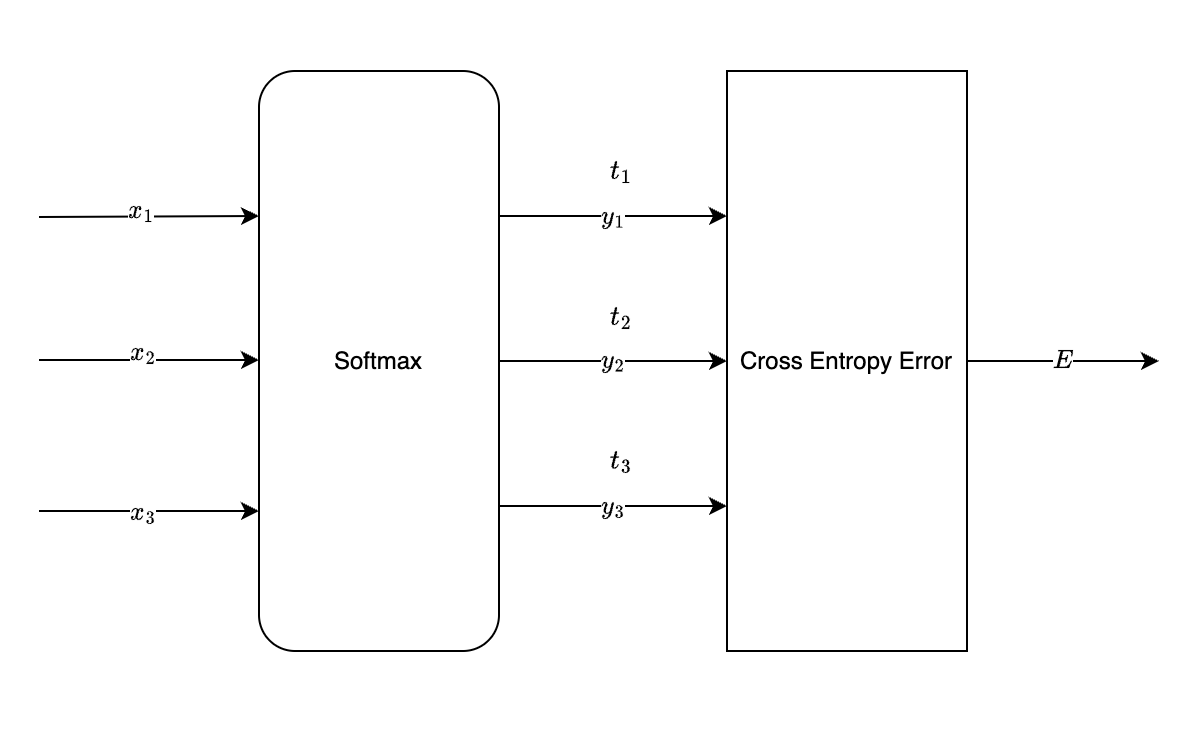
Softmax-with-Loss 层
顾名思义,Softmax-with-Loss 层就是将 Softmax 层和 Loss
函数层结合在一起,以交叉熵分析为例:
事实上,对于一个用于分类的神经网络,softmax
函数只有在学习的过程中会使用,如果只用于判断某个数据的类别,只需要找到最后一层输出层的最大值即可。而如果是在学习的过程中使用了
softmax 函数,那就意味着马上需要计算其损失函数,于是在这里我们直接将
Softmax 层和 Lost 层看成一个整体。
有意思的是将两层看做一个整体后,其偏导数相当简洁: \[
\frac{\partial E}{\partial x_i} = - \frac{\partial}{\partial x_i} \sum_k
t_k\ ln\ \frac{exp(x_i)}{\sum_j exp(x_j)} = \frac{exp(x_i)}{\sum_j
exp(x_j)} \sum_k t_k - t_i = y_i - t_i
\] 代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class SoftmaxWithLoss :def __init__ (self):None None def forward (self, x, t ):return outdef backward (self, dout = 1 ):0 ]return dx
MNIST 示例
接下来我们以 MNIST 数据集为例,展示一次完整的机器学习过程。
MNIST 数据集来自美国国家标准与技术研究所, National Institute of
Standards and Technology(NIST)。训练集(training set)由来自 250
个不同人手写的数字构成, 其中 50% 是高中学生, 50%
来自人口普查局的工作人员。测试集(test set)也是同样比例的手写数字数据。
下载 MNIST
训练集与数据预处理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 from keras.datasets import mnistfrom PIL import Imageimport numpy as npdef show_img (img ):def main ():0 print (t_train[idx]) if __name__ == '__main__' :
直接下载的训练数据 x_train 是
(60000, 28, 28) 的三维数组,且元素是 [0, 256)
的正整数,我们要将其降维以及正规化,同时还要将监督数据转化为 one-hot
形式,因此在训练前要对数据进行预处理:
1 2 3 4 5 6 7 8 def pre_process (x, t ):0 ], shape[1 ] * shape[2 ]) / float (255 )10 ), dtype = np.float64)for i in range (t.size):1 return x_pro, t_pro
1 2 3 4 5 6 7 (x_train, t_train), (x_test, t_test) = mnist.load_data()print (x_train.shape) print (t_train.shape)
基于反向传播的二层神经网络实现
基于先前得到的理论,我们在此处实现一个简单的神经网络:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 class TwoLayerNetWork :def __init__ (self, input_size, hidden_size, output_size, init_std = 0.01 ):'W1' ] = init_std * np.random.randn(input_size, hidden_size)'b1' ] = init_std * np.random.randn(hidden_size)'W2' ] = init_std * np.random.randn(hidden_size, output_size)'b2' ] = init_std * np.random.randn(output_size)'Affine1' ] = Affine(self.params['W1' ], self.params['b1' ])'Relu1' ] = Relu()'Affine2' ] = Affine(self.params['W2' ], self.params['b2' ])def predict (self, x ):for layer in self.layers.values():return xdef loss (self, x, t ):return self.last_layer.forward(y, t)def accuracy (self, x, t ):1 if y.ndim == 2 else 0 )1 if t.ndim == 2 else 0 )return np.sum (y == t) / float (y.size)def numerical_gradient (self, x, t ):lambda w : self.loss(x, t)for key in ('W1' , 'b1' , 'W2' , 'b2' ):return gradsdef gradient (self, x, t ):1 )list (self.layers.values())for layer in layers:'W1' ] = self.layers['Affine1' ].dW'b1' ] = self.layers['Affine1' ].db'W2' ] = self.layers['Affine2' ].dW'b2' ] = self.layers['Affine2' ].dbreturn grads
这里保留了 numerical_gradient()
方法,主要用于在训练前检测反向传播所求解的梯度是否足够准确。
以 MNIST 数据集为例,我们取前 10
个数据,计算两种梯度求法结果的平均差值:
1 2 3 4 5 6 7 8 9 10 11 10 784 , hidden_size = 50 , output_size = 10 )for key in g1.keys():abs (g1[key] - g2[key]))print (key + ':' + str (diff))
控制台输出:
1 2 3 4 W1:3.0029986781580274e-10
误差很小,说明反向传播求解梯度是可行的。
神经网络的学习与测试
我们采取 SGD 对神经网络进行训练,batch_size 设置为
100,迭代数设置为 10000,学习率设置为
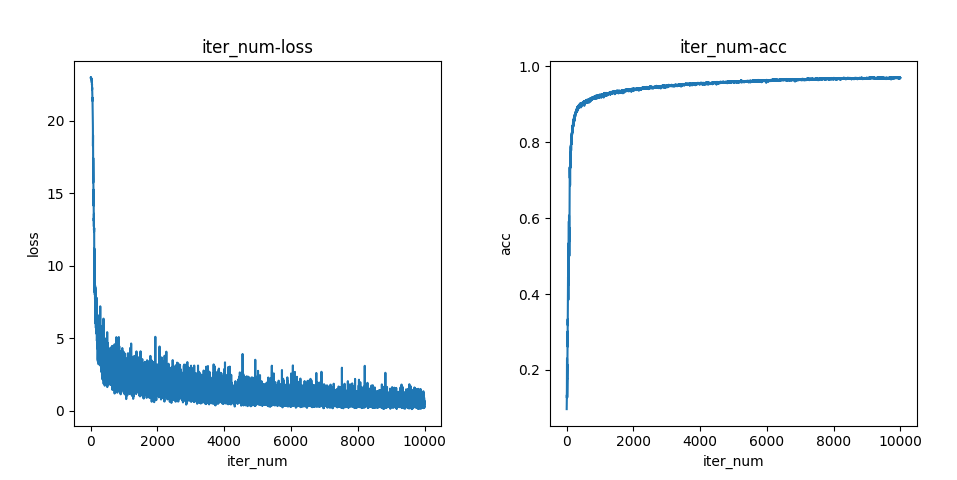
0.1,同时我们记录每轮学习的损失函数以及对测试数据预测的准确率。代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 def train (x_train, t_train, x_test, t_test ):784 , hidden_size = 50 , output_size = 10 )0 ]100 10000 0.1 for i in range (iter_num):for key in nw.params.keys():print ('iter %d, loss = %lf, acc = %lf' % (i, loss, acc))121 )'iter_num' )'loss' )'iter_num-loss' )0 , len (loss_list)), loss_list)122 )'iter_num' )'acc' )'iter_num-acc' )0 , len (acc_list)), acc_list)
结果如下图:
学习的效果总体呈现为先快后慢的趋势,损失函数逐渐趋于
0,预测准确率逐渐趋于 1。在一万次迭代后,预测准确率可以达到约 \(97 \%\) 。这样,我们就完成了 MINIST
数据集的学习过程了。
神经网络学习技巧
更优的梯度下降策略
神经网络的学习目的可以概括为找到使损失函数的值尽可能小的参数。这个过程被称为最优化(Optimization) 。
前几章我们讨论了随机梯度下降法(Stochastic Gradient
Descent) ,即 SGD。
本章我们将讨论其他优化的梯度下降法。
SGD 的缺点
如果函数的形状非均向(anisotropic) ,收敛会很慢。
以函数 \(f(x, y) = \frac{1}{100} x^2 +
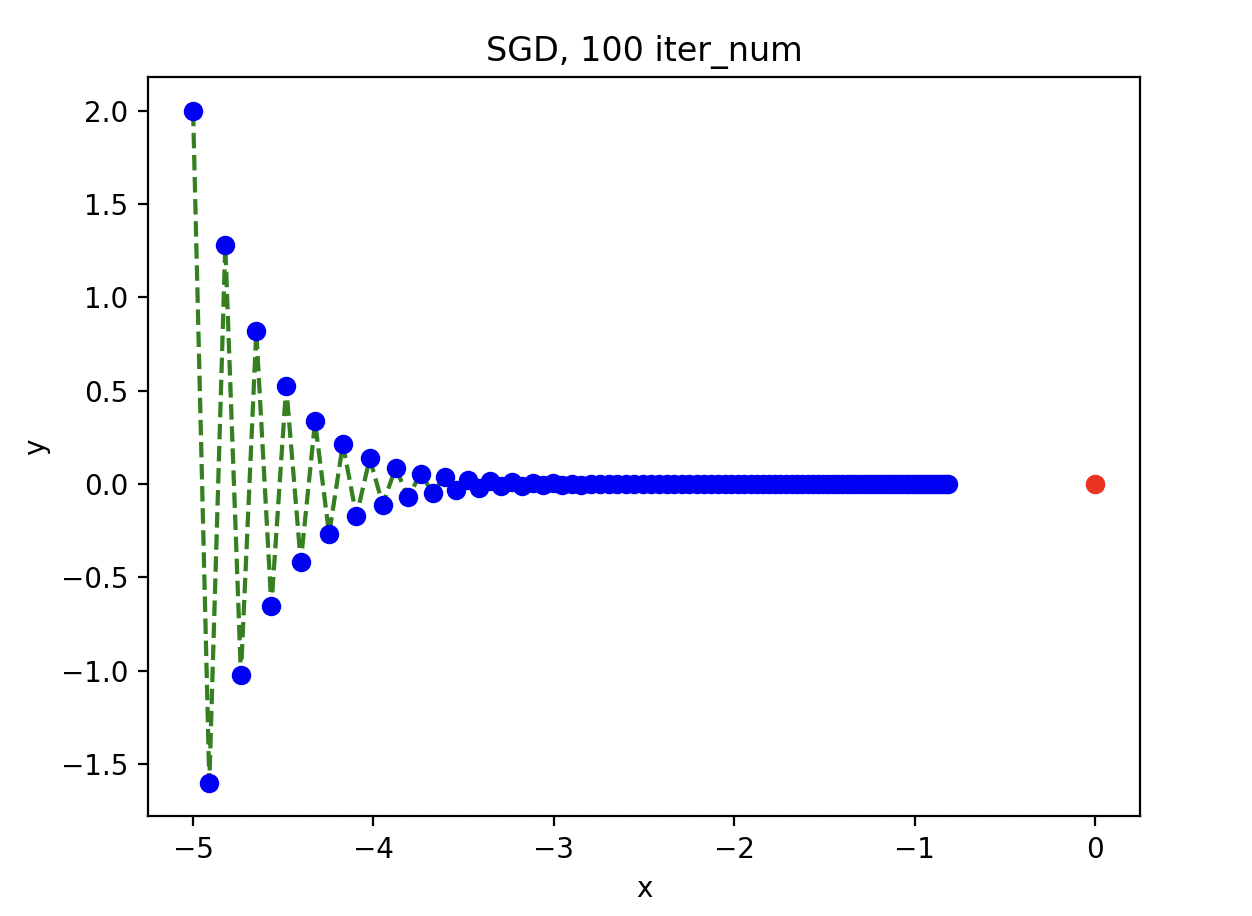
y^2\) 为例子,我们采取 SGD 方法求其最小值,假设初始值为 \((-5, 2)\) 。
1 2 3 4 dat = np.array([-5 , 2 ], dtype = np.float64)lambda dat : 1 / 100 * dat[0 ] ** 2 + dat[1 ] ** 2 for i in range (iter_num):
结果如下:
如上图所示,在 100 次迭代后仍然离极小值点 \((0, 0)\)
有一定距离,最后参数的移动路径近似于 Z 字形,收敛十分缓慢。
可见,随机梯度下降在本例中效率很低。从数学的层面理解,可以认为是 x
的梯度分量过小导致的。
Momentum
Momentum ,即动量,相当于我们给梯度下降引入了物理规则,具体算法如下:
\[
\begin{array}{}
v := \alpha v - \eta \frac{\partial L}{\partial W} \\
W := W + v
\end{array}
\] \(W\) 表示参数,\(v\)
在这里是一个新的变量,用于表示速度。
\(\eta\) 表示学习率,\(\alpha\)
表示衰减率。不同于常规的梯度下降,动量梯度下降使用速度对参数进行更新,可以使得目标更快朝极小值点移动。
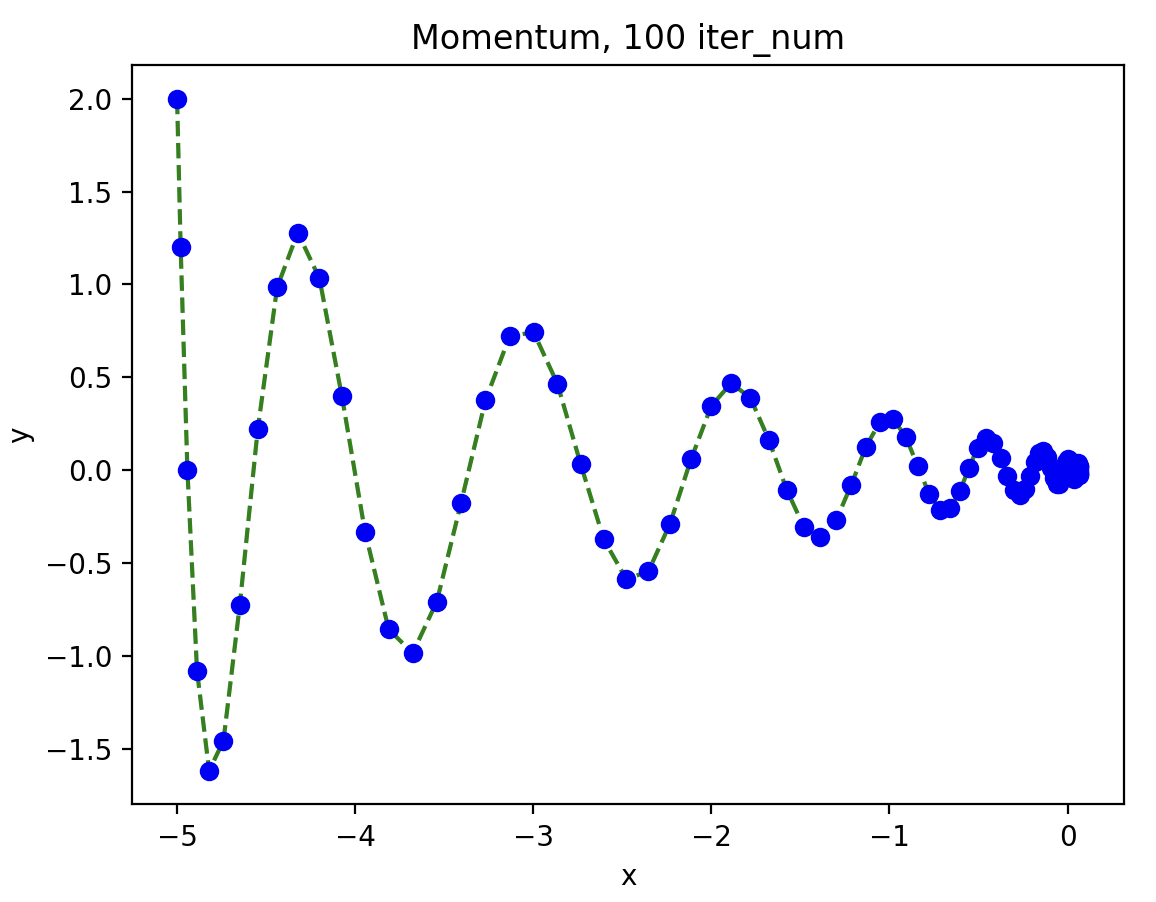
还是以刚才我们讨论的函数为例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Momentum :def __init__ (self, lr = 0.1 , mom = 0.9 ):None def update (self, params, grads ):if self.v is None :lambda dat : 1 / 100 * dat[0 ] ** 2 + dat[1 ] ** 2 0.2 )for i in range (iter_num):
可见,动量梯度下降路径更为平缓,且在有限次迭代中更快收敛至极小值点。
相较于 SGD,动量梯度下降为何能做到更快收敛呢?
AdaGrad
在神经网络的学习中,学习率的选取非常重要。学习率过小,可能导致学习花费时长过多,学习率过大,可能导致学习过程无法收敛。所以我们给出
AdaGrad,即适应性调整学习率的梯度下降。
我们引入学习衰减率(Learning Rate Decay) \(h\)
,使得随着学习进行,学习率逐渐减小。
数学表示如下: \[
\begin{array}{}
h := h + \frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial
W} \\
W := W - \eta \frac{1}{\sqrt h} \frac{\partial L}{\partial W}
\end{array}
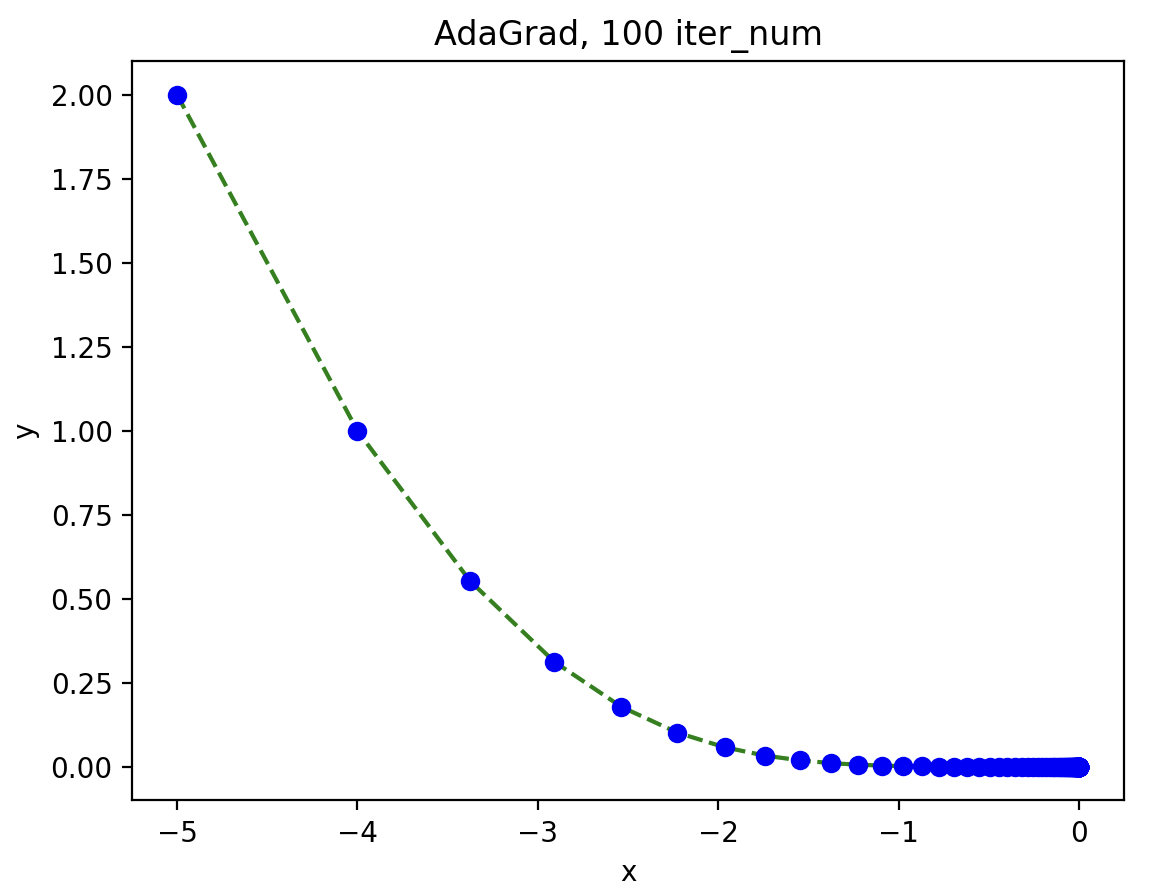
\] 还是以上述函数为例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class AdaGrad :def __init__ (self, lr = 0.1 ):None def update (self, params, grads ):if self.h is None :1e-7 lambda dat : 1 / 100 * dat[0 ] ** 2 + dat[1 ] ** 2 1 )for i in range (iter_num):
AdaGrad
的思路其实就是将更新过程中变化较大的参数的学习率降低,从而调整学习的尺寸。整体而言都是先快后慢,但如果无止境地学习,更新速度就会变成
0。为了改善这个问题,可以使用 RMSProp 方法。
关于权重的初始值
权重初始值是否可以设置为 0 ?
答案是否定的,假设初始状态权重为
0,则第二层神经元会被传递相同的值,第二层神经元全部输入相同的值,这意味着反向传播时第二层的权重会进行相同的更新。这样一来,权重将会维持均一化,为了防止这种情况发生,必须随机生成初始值。
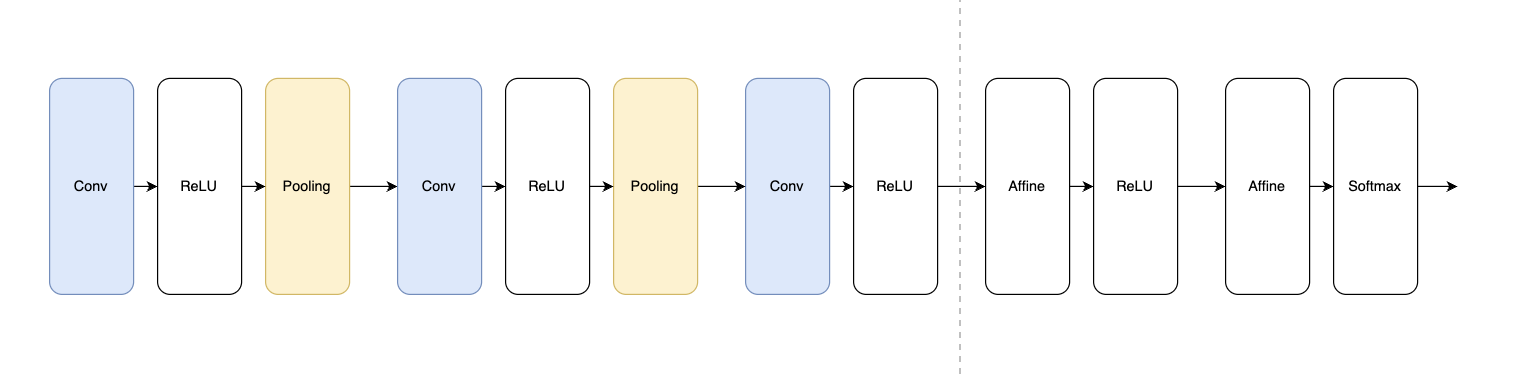
卷积神经网络
整体结构
卷积神经网络(Convolutional Nerual Network) ,简称
CNN 神经网络 ,相比于全连接神经网络,CNN
神经网络新出现了卷积(Convolution)层和池化(Pooling)层。
卷积层
卷积运算
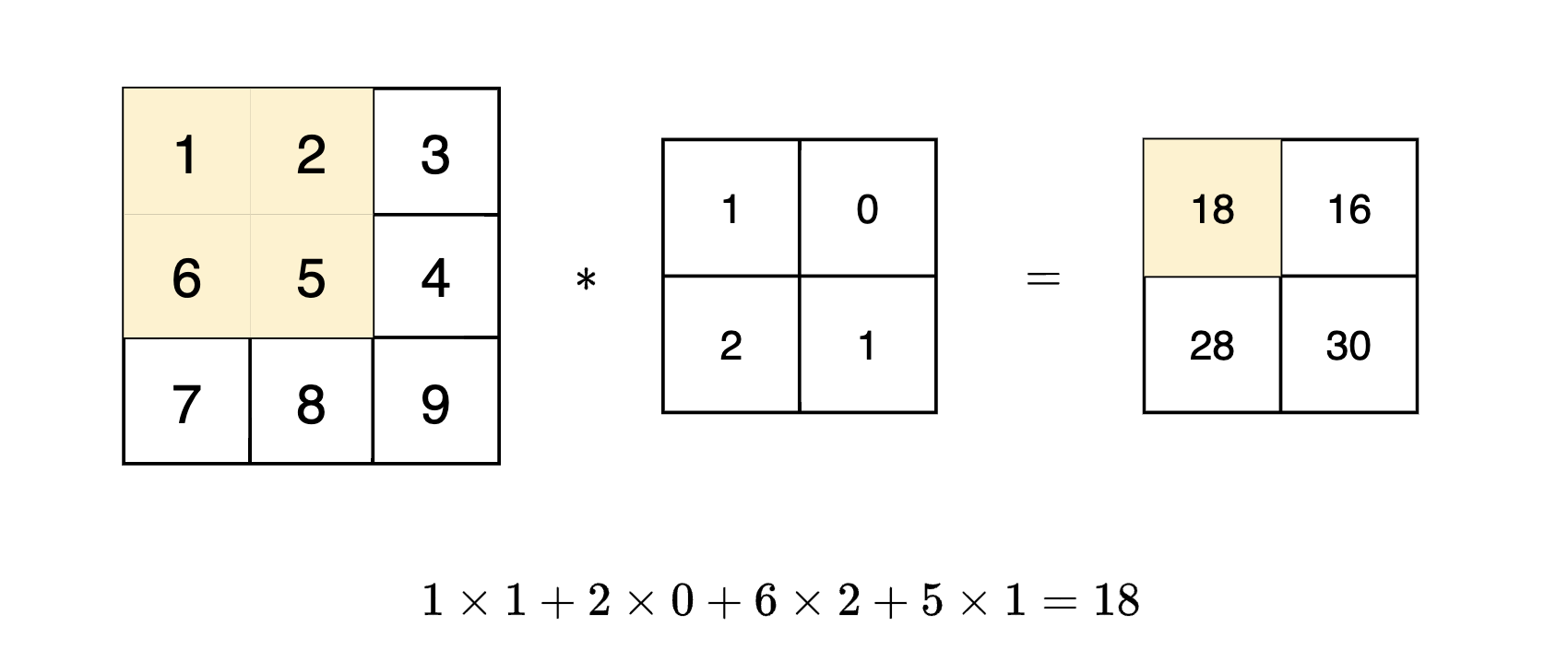
卷积层进行的处理就是卷积运算。卷积运算相当于图像处理中的
“滤波器运算”。
如上图,卷积运算以一定间隔滑动滤波器的窗口,每次将滤波器的元素和输入的对应元素相乘然后求和,将这个结果保存到输出的对应位置,就可以得到卷积的结果。
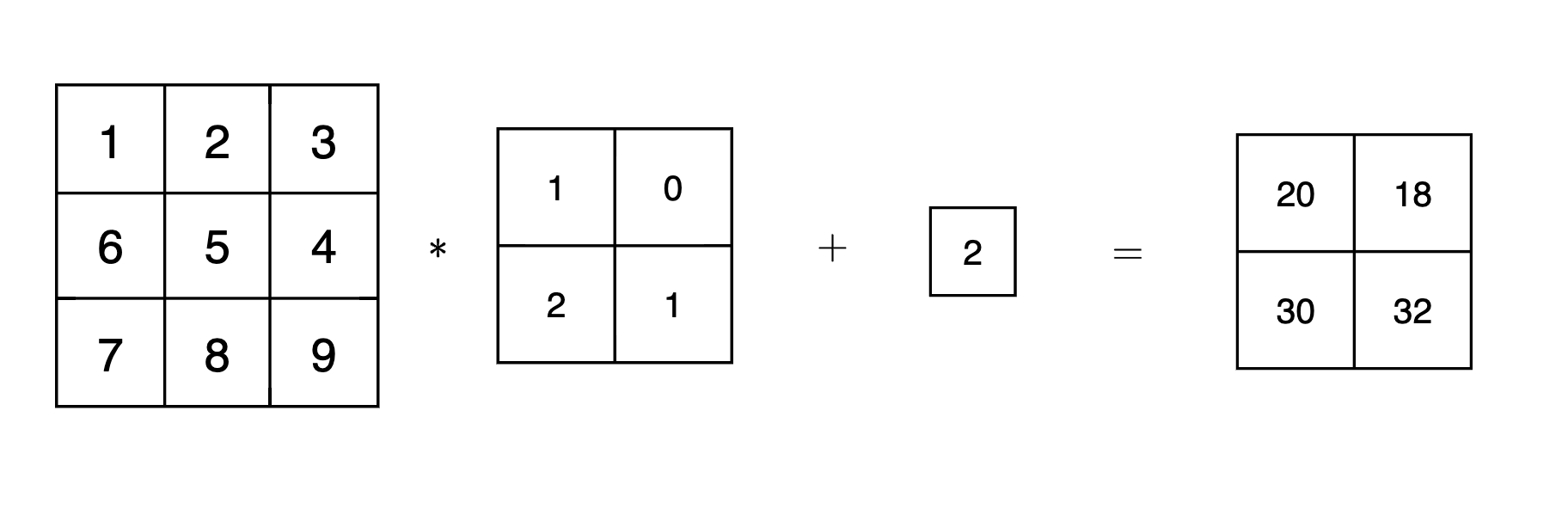
对于 CNN 神经网络而言,卷积运算结束后一般会加上一个偏置,如下图:
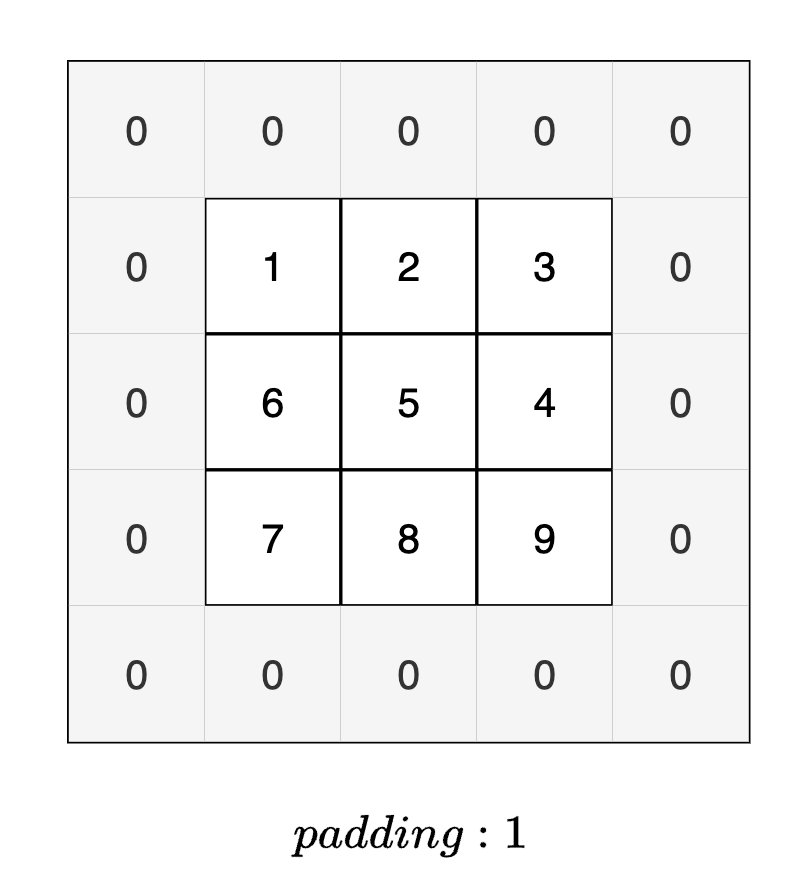
填充
在进行卷积运算的处理之前,有时要向输入数据的周围填入固定的数据,比如
0
等,这就称为填充(padding) 。通过合适的填充,可以保证卷积运算后的结果相对于输入空间大小不变。
步幅
应用滤波器的位置间隔称为步幅(stride) ,前面的例子中,滤波器的步幅都为
1,若步幅设置为 2,则滤波器每次移动 2 个像素。
假设输入大小为 \((H, W)\) ,填充为
\(P\) ,步幅为 \(S\) ,滤波器大小为 \((FH, FW)\) 。
设输出大小为 \((OH, OW)\) ,则有:
\[
OH = \frac{H + 2P - FH}{S} + 1
\]
\[
OW = \frac{W + 2P - FW}{S} + 1
\]
三维数据的卷积运算
相对于二维数据的卷积运算,三维卷积运算除了处理长、宽之外还要处理通道方向。通道方向有多个特征图时,会按照通道进行数据和滤波器的卷积运算,然后相加。
输入数据和滤波器的通道数必须相等,输出数据会得到一张特征图,即通道数为
1
的输出数据。如果要在通道方向也拥有多个卷积运算的输出,就需要多个滤波器。
假设输入数据大小为 \((C, H, W)\)
,即通道数为 \(C\) ,高为 \(H\) ,宽为 \(W\) ;滤波器数据大小为 \((FN, C, FH, FW)\) ,即滤波器个数为 \(FN\) 个,通道数为 \(C\) ,高为 \(FH\) ,宽为 \(FW\) ;则输出数据的大小可以表示为 \((FN, OH, OW)\)
,即输出数据的通道数为滤波器的数量 \(FN\) 。
池化层
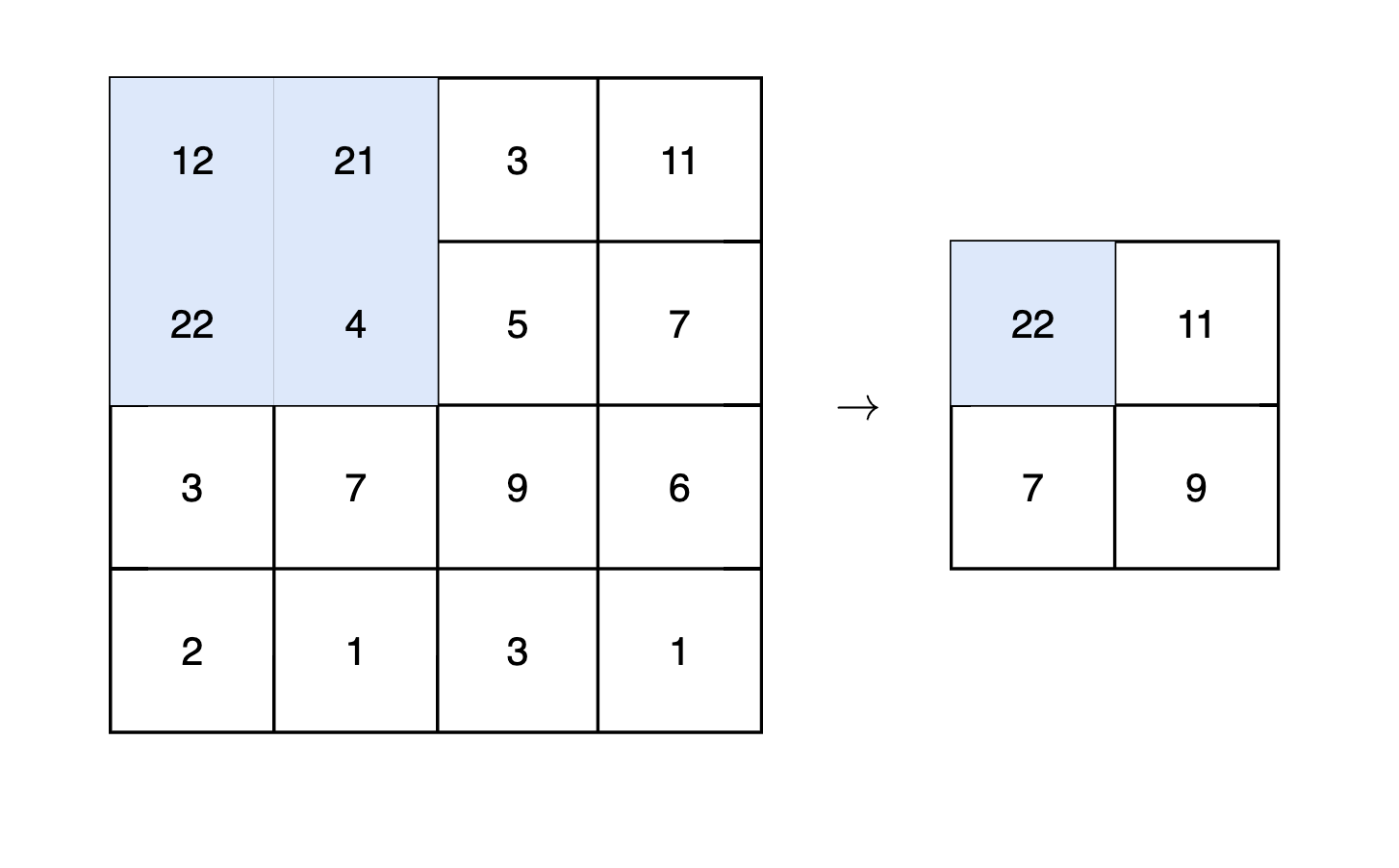
池化是缩小高、宽方向上空间的操作。常见的池化有 Max 池化和 Average
池化。
对于一个 \(n \times n\) 的 Max
池化操作,每次选取一个 \(n \times n\)
的区域,从该区域中取出最大值并记录到最终答案。一般而言,步幅和池化窗口大小会设置为同样的值。
下图演示了一个 \(2 \times 2\)
的池化操作:
池化层具有以下特征:
没有需要学习的参数;
通道数不发生变化;
对微小的位置变化具有鲁棒性。
若输入数据发生微小变化时,池化仍然会返回相同的结果。例如 Max
池化,只要在池化区域内的最大值不发生变化,那么池化就可以吸收数据的偏差,仍然返回相同的结果。
卷积层和池化层的代码实现
4 维数组
由于 CNN 各层间传递的是 4 维数据,所以我们需要用 4
维数组来存储参数:
1 2 x = np.random.rand(n, c, h, w)
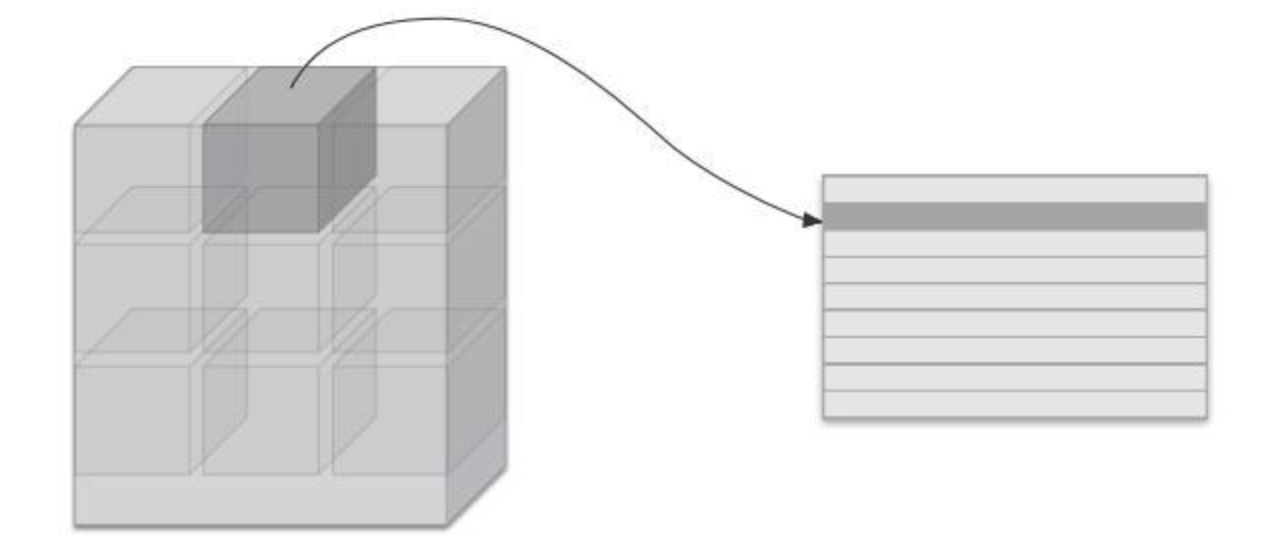
im2col 技巧如果只是按照平常的卷积运算,则会出现好几层 for
循环,十分不利于代码的书写,我们可以考虑 im2col
技巧,把输入数据按照滤波器的作用区域进行展开:
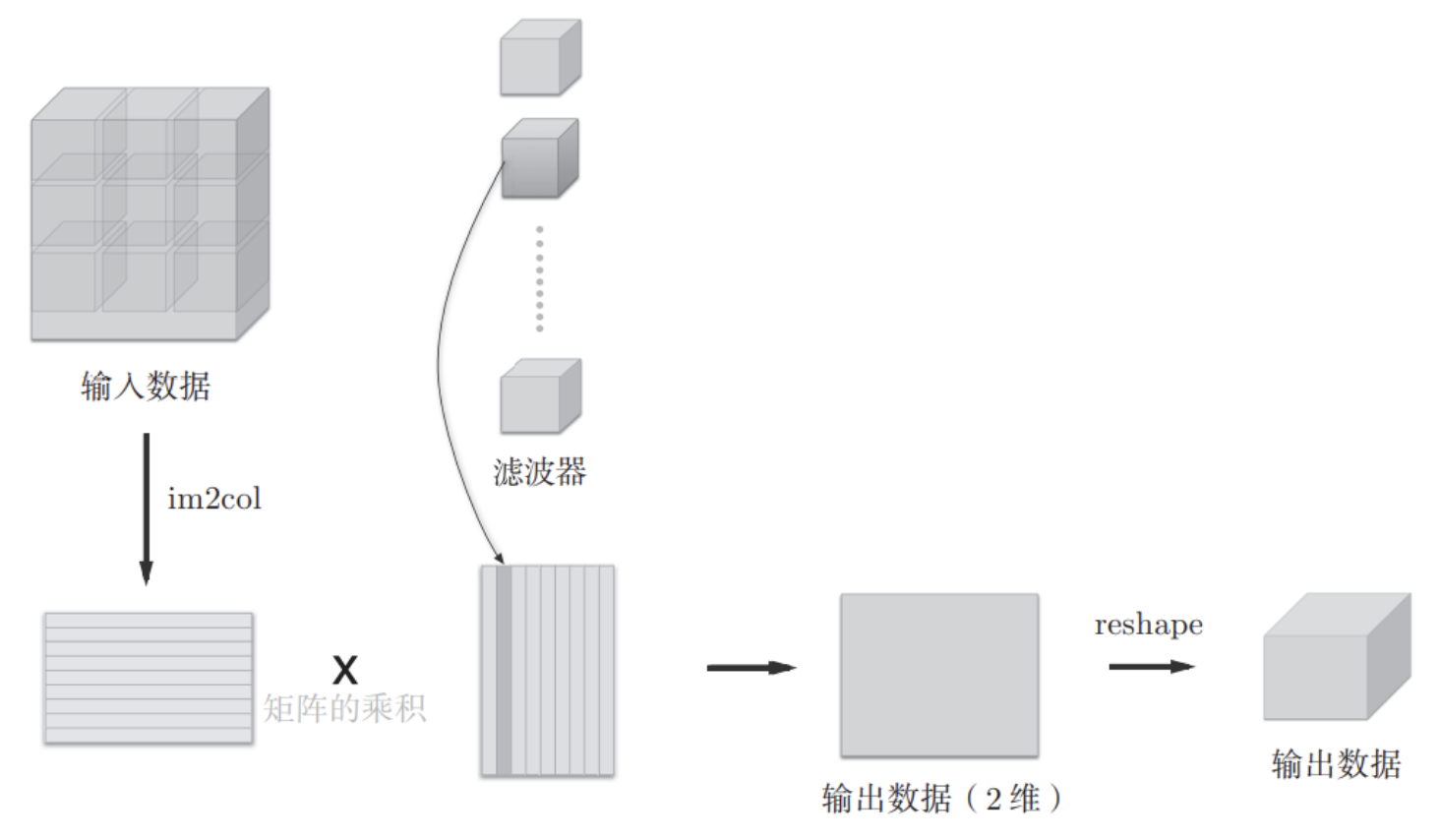
此后就可以将卷积运算汇总为一个大的矩阵乘积,而在 Numpy
库中,矩阵计算都进行过高度优化,因此我们可以实现更高效的计算。
代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 def im2col (input_data, filter_h, filter_w, stride = 1 , pad = 0 ):""" Parameters ---------- input_data : 由(数据量, 通道, 高, 长)的4维数组构成的输入数据 filter_h : 滤波器的高 filter_w : 滤波器的长 stride : 步幅 pad : 填充 Returns ------- col : 2维数组 """ 2 * pad - filter_h) // stride + 1 2 * pad - filter_w) // stride + 1 0 , 0 ), (0 , 0 ), (pad, pad), (pad, pad)], "constant" )for y in range (filter_h):for x in range (filter_w):0 , 4 , 5 , 1 , 2 , 3 ).reshape(N * out_h * out_w, -1 )return col
卷积层实现
利用上述 im2col 技巧,我们就可以实现卷积层了:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class Convolution :def __init__ (self, W, b, stride = 1 , pad = 0 ):None None None None None def forward (self, x ):1 + int ((H + 2 * self.pad - FH) / self.stride)1 + int ((W + 2 * self.pad - FW) / self.stride)1 ).T1 ).transpose(0 , 3 , 1 , 2 )return outdef backward (self, dout ):0 , 2 , 3 , 1 ).reshape(-1 , FN)sum (dout, axis=0 )1 , 0 ).reshape(FN, C, FH, FW)return dx
事实上使用 im2col 后的卷积层与 Affine
层的实现是差不多的,这里在反向传播的时候需要使用 im2col 的逆操作 col2im
来恢复数组。
池化层实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Pooling :def __init__ (self, pool_h, pool_w, stride=1 , pad=0 ):None None def forward (self, x ):int (1 + (H - self.pool_h) / self.stride)int (1 + (W - self.pool_w) / self.stride)1 , self.pool_h * self.pool_w)1 )max (col, axis=1 )0 , 3 , 1 , 2 )return outdef backward (self, dout ):0 , 2 , 3 , 1 )0 ] * dmax.shape[1 ] * dmax.shape[2 ], -1 )return dx
CNN 的代码实现
基于上述讨论,我们就可以实现一个完整的 CNN 神经网络了:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 class SimpleConvNet :"""简单的ConvNet conv - relu - pool - affine - relu - affine - softmax Parameters ---------- input_size : 输入大小(MNIST的情况下为784) hidden_size_list : 隐藏层的神经元数量的列表(e.g. [100, 100, 100]) output_size : 输出大小(MNIST的情况下为10) activation : 'relu' or 'sigmoid' weight_init_std : 指定权重的标准差(e.g. 0.01) 指定'relu'或'he'的情况下设定“He的初始值” 指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值” """ def __init__ ( self, input_dim=(1 , 28 , 28 conv_param={"filter_num" : 30 , "filter_size" : 5 , "pad" : 0 , "stride" : 1 }, hidden_size=100 , output_size=10 , weight_init_std=0.01 , ):"filter_num" ]"filter_size" ]"pad" ]"stride" ]1 ]2 * filter_pad1 int (2 ) * (conv_output_size / 2 )"W1" ] = weight_init_std * np.random.randn(0 ], filter_size, filter_size"b1" ] = np.zeros(filter_num)"W2" ] = weight_init_std * np.random.randn("b2" ] = np.zeros(hidden_size)"W3" ] = weight_init_std * np.random.randn(hidden_size, output_size)"b3" ] = np.zeros(output_size)"Conv1" ] = Convolution("W1" ],"b1" ],"stride" ],"pad" ],"Relu1" ] = Relu()"Pool1" ] = Pooling(pool_h = 2 , pool_w = 2 , stride = 2 )"Affine1" ] = Affine(self.params["W2" ], self.params["b2" ])"Relu2" ] = Relu()"Affine2" ] = Affine(self.params["W3" ], self.params["b3" ])def predict (self, x ):for layer in self.layers.values():return xdef loss (self, x, t ):"""求损失函数 参数x是输入数据、t是教师标签 """ return self.last_layer.forward(y, t)def accuracy (self, x, t, batch_size = 100 ):if t.ndim != 1 :1 )0.0 for i in range (int (x.shape[0 ] / batch_size)):1 ) * batch_size]1 ) * batch_size]1 )sum (y == tt)return acc / x.shape[0 ]def numerical_gradient (self, x, t ):"""求梯度(数值微分) Parameters ---------- x : 输入数据 t : 教师标签 Returns ------- 具有各层的梯度的字典变量 grads['W1']、grads['W2']、...是各层的权重 grads['b1']、grads['b2']、...是各层的偏置 """ lambda w: self.loss(x, t)for idx in (1 , 2 , 3 ):"W" + str (idx)] = numerical_gradient("W" + str (idx)]"b" + str (idx)] = numerical_gradient("b" + str (idx)]return gradsdef gradient (self, x, t ):"""求梯度(误差反向传播法) Parameters ---------- x : 输入数据 t : 教师标签 Returns ------- 具有各层的梯度的字典变量 grads['W1']、grads['W2']、...是各层的权重 grads['b1']、grads['b2']、...是各层的偏置 """ 1 list (self.layers.values())for layer in layers:"W1" ], grads["b1" ] = self.layers["Conv1" ].dW, self.layers["Conv1" ].db"W2" ], grads["b2" ] = self.layers["Affine1" ].dW, self.layers["Affine1" ].db"W3" ], grads["b3" ] = self.layers["Affine2" ].dW, self.layers["Affine2" ].dbreturn gradsdef save_params (self, file_name="params.pkl" ):for key, val in self.params.items():with open (file_name, "wb" ) as f:def load_params (self, file_name="params.pkl" ):with open (file_name, "rb" ) as f:for key, val in params.items():for i, key in enumerate (["Conv1" , "Affine1" , "Affine2" ]):"W" + str (i + 1 )]"b" + str (i + 1 )]
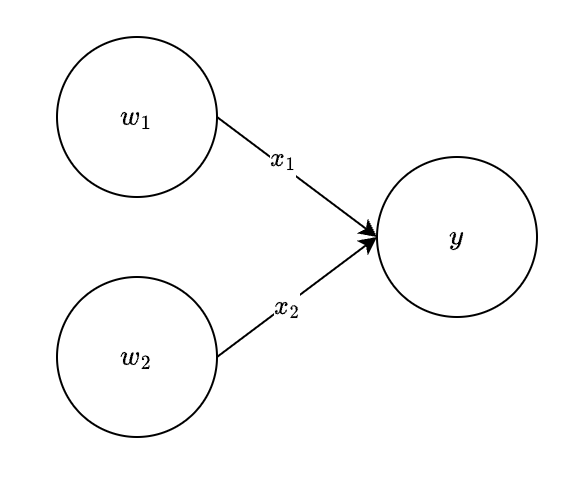 \[
\begin{equation}
y =
\begin{cases}
0 & (w_1 x_1 + w_2 x_2 \leq 0) \\
1 & (w_1 x_1 + w_2 x_2 > 0)
\end{cases}
\end{equation}
\] 而神经网络就是由很多层复杂的感知机组合而成的。
\[
\begin{equation}
y =
\begin{cases}
0 & (w_1 x_1 + w_2 x_2 \leq 0) \\
1 & (w_1 x_1 + w_2 x_2 > 0)
\end{cases}
\end{equation}
\] 而神经网络就是由很多层复杂的感知机组合而成的。