如何在程序中计算定积分？—— Simpson 公式讲解

Simpson 公式是一种用于求积分近似值的方法，相对于常规的矩形逼近和梯型逼近，其精度要高很多。

公式如下： \[ \int_a^b f(x)dx \approx \frac{b - a}{6n} (f(a) + f(b) + 2 \sum_{i = 1} ^ {n - 1}f(x_i) + 4 \sum_{i = 0}^{n - 1}f(x_{i + 0.5})) \] 其中 \(n\) 是区间分隔的数量，\(n\) 越大，精度越高。

---

数学证明

Simpson 积分公式的原理就是采用二次函数逼近目标函数。

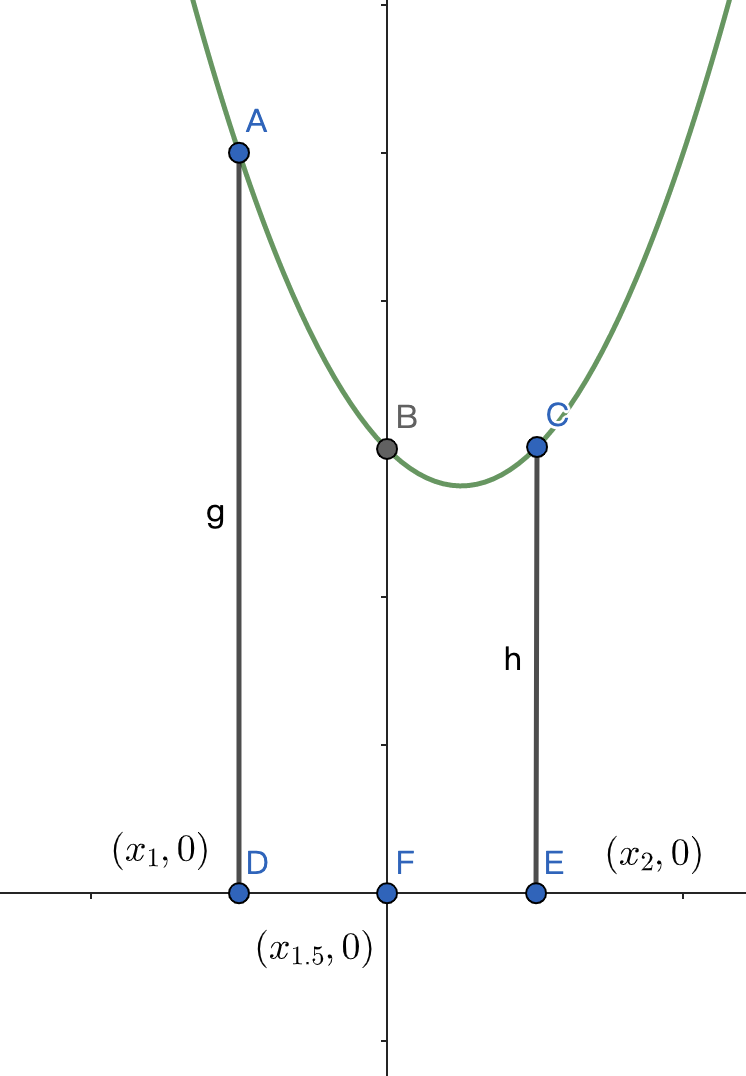
如上图所示，我们将函数区间 \([x_1, x_2]\) 近似看作是二次函数，\(x_{1.5}\) 是区间中点，我们规定： \[ \begin{array}{} f(x_1) = c_2 x_1^2 + c_1 x_1 + c_0 \\ f(x_2) = c_2 x_2^2 + c_1 x_2 + c_0 \\ f(x_{1.5}) = c_0 \end{array} \] 则积分面积 \(S = \int_{x_1}^{x_2} f(x)dx \approx \int_{x_1}^{x_2} (c_2 x^2 + c_1 x + c_0)dx\) \[ \begin{array}{} \implies S \approx \frac{c_2}{3}(x_2^3 - x_1^3) + \frac{c1}{2}(x_2^2 - x_1^2) + c_0(x_2 - x_1) \\ = \frac{x_2 - x_1}{6}(f(x_1) + f(x_2) + 4 f(x_{1.5})) \end{array} \] 现在我们将函数积分区域 \([a, b]\) 划分为 \(n\) 段，对每一段 \([x_i, x_{i + 1}]\) 采取同样的方式求定积分，

最后求和就可以得到我们的目标答案： \[ \begin{array}{} \int_a^b f(x)dx \approx \frac{b - a}{6n} (f(a) + f(b) + 2 \sum_{i = 1} ^ {n - 1}f(x_i) + 4 \sum_{i = 0}^{n - 1}f(x_{i + 0.5})) \\ (x_0 = a, x_n = b) \end{array} \] 误差

最大误差为 \(\frac{(b - a)^5}{180 n^4} M\)，其中 \(M\) 是函数在区间 \([a, b]\) 上四阶导的绝对值的最大值。

代码实现

#include <cstdio>
#include <cmath>

inline double fn(double x) {
    return x * exp(-x);
}

double solve_rect(double left, double right, int n) {
    // 采用一般的矩形逼近法求定积分
    double res = 0;
    double d = (right - left) / n;
    for (int i = 0; i < n; i++) {
        res += fn(left + i * d);
    }

    return res * d;
}

double solve_simpson(double left, double right, int n) {
    // 采取辛普森公式求定积分
    double res = -fn(left) + fn(right);
    double d = (right - left) / n;
    for (int i = 0; i < n; i++) {
        res += (2 * fn(left + i * d) + 4 * fn(left + (i + 0.5) * d));
    }

    return d * res / 6;
}

int main() {

    printf("%lf\n", solve_rect(0, 1, 10));      // 0.245014
    printf("%lf\n", solve_rect(0, 1, 100));     // 0.262393
    printf("%lf\n", solve_rect(0, 1, 1000));    // 0.264057

    printf("%lf\n", solve_simpson(0, 1, 10));   // 0.264241

    return 0;
}

实际答案 \(\int_0^1 x e^{-x}dx = 1 - \frac{2}{e} \approx 0.2642411176571\)，可见上述积分采用 Simpson 公式计算时在 \(n = 10\) 时已经达到了一个较高的精度，远超常规的矩形逼近法。