二分匹配问题 —— 匈牙利算法

问题介绍

什么是二分图？

对于图 \(G(V,E)\) 而言，若 \(G\) 中的所有点可以划分为两个子集 \(G_1\)、\(G_2\) ，且图中每条边 \(e\) 关联的两个顶点都属于不同的顶点子集，这样的图我们称为二分图（ Bipartite Graph ），或者二部图。

最大匹配问题和最小点覆盖问题

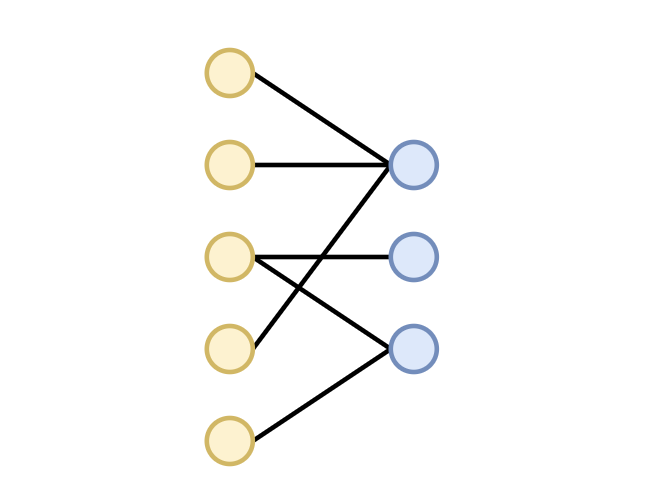
什么是最大匹配问题？给定一个二分图 \(G(V,E)\)，若 \((a_i,b_j) \in E\) ，我们就称 \(a_i\) 和 \(b_j\) 是可配对的，已知该图中任意顶点至多匹配一个顶点，求最大匹配数。如下图，不难看出该图的最大匹配数为 2。其中一种匹配方式为 \((a_1, b_1)\)、\((a_3, b_4)\) 。

什么又是最小点覆盖问题呢？即从二分图中删除最少的顶点，使得图 \(G\) 中任何一对点都无法匹配。删除顶点的最小数量称为最小点覆盖数。如下图，不难看出最小覆盖数也是 2。我们可以删去 \(a_3\) 和 \(b_1\) 使得图中任何一对点都无法匹配。

这两个问题看似不一样，实际上实际上是处理一个相同的问题。为什么这么说呢？因为我们可以证明一条重要性质：

最大匹配数 = 最小覆盖数

具体证明就不在这里说明了，笔者打算以后单独出一期文章来证明该性质。

那我们该如何给出二分匹配问题的一般解决方案呢？1955 年，库恩（ W.W.Kuhn ）利用一个匈牙利数学家康哥尼（ D.Kőnig ）的一个定理构造了一种二分匹配问题的解法，后人称之为匈牙利算法。

匈牙利算法

在介绍匈牙利算法之前，我们先介绍几个概念：

交替路：

从未匹配点出发，依次经过未匹配的边和已匹配的边的路径称为交替路。
增广路：

经过除出发点之外其他未匹配点的交替路称为增广路。

当且仅当不存在关于图 \(G\) 的增广路径时当前的匹配为图 \(G\) 的最大匹配。

算法讲解

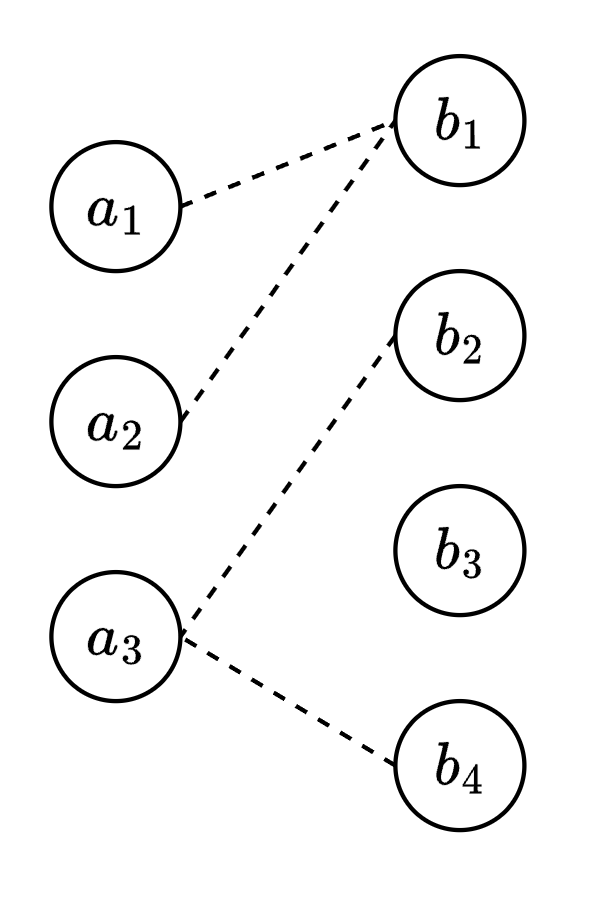
如下图所示，我们接下来将使用匈牙利算法来计算该二分图的最大匹配数。

我们从 \(a_1\) 开始匹配，\(a_1\) 与 \(b_1\) 匹配成功，即当前匹配对数为 1。

(1) (2)

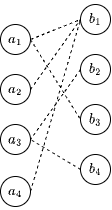
然后再对 \(a_2\) 进行匹配，我们发现 \(a_2\) 只能匹配 \(b_1\) ，而 \(b_1\) 已经与 \(a_1\) 匹配成功了，此时我们发现 \(a_1\) 和 \(b_3\) 可以成功匹配，于是我们可以取消 \(a_1\) 和 \(b_1\) 的匹配，然后匹配 \(a_1\) 和 \(b_3\) ，这个时候 \(a_2\) 就可以匹配 \(b_1\) 了。匹配对数加一，当前匹配对数为 2。

其实这一步相当于找到了一条增广路 \((a_2, b_1, a_1, b_3)\) ，然后对该增广路取反。

(3)

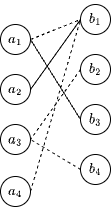
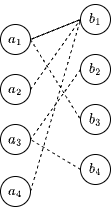
接下来对 \(a_3\) 进行匹配，\(a_3\) 与 \(b_2\) 成功匹配，匹配对数加一，当前匹配对数为 3。

(4)

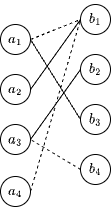
最后对 \(a_4\) 进行匹配，发现其只能与 \(b_1\) 匹配，而 \(b_1\) 已经与 \(a_1\) 匹配过了，而且无法从 \(a_4\) 出发构造一条增广路，因此 \(a_4\) 无法与任何一个顶点成功匹配。

综上所述，展示的二分图的最大匹配数为 3。

伪代码：

// 判断 ai 是否能匹配成功
for bj 与 ai 相连:
		if bj 未被访问:
				更新 bj 访问状态;
        if bj 未被匹配或者 bj 的配对点可以出发找到增广路径:
        		将 bj 的配对点改为 ai;
        		return true;

return false;

时间复杂度：\(O(VE)\)

代码实现

#define NOT_MATCH 0x3f3f3f3f

class Solution {
private:
  	int numA, numB; // numA、numB 分别表示两个集合的元素个数
  	vector<vector<int>> G; // 假设这里用邻接链表储存图 G，G[i] 表示和 ai 相邻的所有 B 集合的顶点编号
  	int match[numB]; // 记录 B 集合的元素的匹配点在 A 集合的编号
  	bool vis[numB]; // 记录 B 集合的元素是否被访问过
		
  	// ...
  	bool isMatch(int index) {
      	// 判断 A 集合中编号为 index 的顶点是否能匹配成功
      	for (int i = 0; i < G[index].size(); i++) {
          	if (!vis[G[i]]) {
              	vis[G[i]] = true;
              	if (match[G[i]] == NOT_MATCH || isMatch(match[[G[i]]])) {
                		// 该顶点未被匹配或着原来匹配该点的顶点可以匹配其他顶点
                  	match[G[i]] = index;
                  	return true;
                }
            }
        }
      	
      	return false;
    }
  
public:
  	int hungarian() {
      	int cnt = 0;
      	for (int i = 0; i < numA; i++) {
          	memset(vis, 0x3f, sizeof(vis));
          	if (isMatch(i)) {
              	cnt++;
            }
        }
      
      	return cnt;
    }
}

实际应用

Machine Schedule

Problem Description As we all know, machine scheduling is a very classical problem in computer science and has been studied for a very long history. Scheduling problems differ widely in the nature of the constraints that must be satisfied and the type of schedule desired. Here we consider a 2-machine scheduling problem.

There are two machines A and B. Machine A has n kinds of working modes, which is called \(mode_0\) , \(mode_1\) , …, \(mode_{n-1}\) , likewise machine B has m kinds of working modes, \(mode_0\), \(mode_1\) , … , \(mode_{m-1}\) . At the beginning they are both work at \(mode_0\).

For k jobs given, each of them can be processed in either one of the two machines in particular mode. For example, job 0 can either be processed in machine A at \(mode_3\) or in machine B at \(mode_4\) , job 1 can either be processed in machine A at \(mode_2\) or in machine B at \(mode_4\) , and so on. Thus, for job i, the constraint can be represent as a triple (i, x, y), which means it can be processed either in machine A at \(mode_x\), or in machine B at \(mode_y\) .

Obviously, to accomplish all the jobs, we need to change the machine’s working mode from time to time, but unfortunately, the machine’s working mode can only be changed by restarting it manually. By changing the sequence of the jobs and assigning each job to a suitable machine, please write a program to minimize the times of restarting machines.

Input The input file for this program consists of several configurations. The first line of one configuration contains three positive integers: n, m (n, m < 100) and k (k < 1000). The following k lines give the constrains of the k jobs, each line is a triple: i, x, y.

The input will be terminated by a line containing a single zero.

Output The output should be one integer per line, which means the minimal times of restarting machine.

输入案例：
1
2
3
4
5
6
7
8
9
10
11
12
5 5 10
0 1 1
1 1 2
2 1 3
3 1 4
4 2 1
5 2 2
6 2 3
7 2 4
8 3 3
9 4 3
0
输出案例：
1
3

对于此题，我们可以将 A、B 机器的所有模式看成二部图看成两个子集，若某个工作需要机器 A 的 x 模式和机器 B 的 y 模式来完成，就将 \((a_x, b_y)\) 连接起来。最后我们的问题就变成了：应该如何找到该二部图的最小点覆盖数？

而根据我们之前提到的结论可知，最小点覆盖数在数值上等于最大匹配数。

代码：

#include <iostream>
#include <cstring>

using namespace std;

#define MAX_NUM 105
#define NOT_FOUND 0x3f3f3f3f

int G[MAX_NUM][MAX_NUM];
bool vis[MAX_NUM];
int match[MAX_NUM];

int n, m, k;

bool isMatch(int index) {
    for (int i = 0; i < m; i++) {
        if (G[index][i] && !vis[i]) {
            vis[i] = true;
            if (match[i] == NOT_FOUND || isMatch(match[i])) {
                match[i] = index;
                return true;
            }
        }
    }

    return false;
}


int main() {

    ios::sync_with_stdio(false);

    while (cin >> n) {
        if (n == 0) {
            break;
        }
        cin >> m >> k;
        memset(G, 0, sizeof(G));
        memset(match, 0x3f, sizeof(match));
        // 初始化
        int t, ax, by;
        for (int i = 0; i < k; i++) {
            cin >> t >> ax >> by;
            if (ax != 0 && by != 0) {
                // 0 号模式下可以完成的任务不用添加
                G[ax][by] = 1;
            }
        }
        int cnt = 0;
        for (int i = 0; i < n; i++) {
            memset(vis, 0, sizeof(vis));
            if (isMatch(i)) {
                cnt++;
            }
        }
        // 求出最小点覆盖数

        cout << cnt << endl;
    }

    return 0;
}

二分图博弈问题

二分图博弈是一类博弈模型，他可以抽象为：给出一张二分图和起点 \(S\) ，两人轮流进行操作，每次操作只能选择与上一个被选的点相邻的点，且不能选择已经选择过的点，无法选点的人输掉。问先手是否必胜。

结论：考虑二分图的所有最大匹配，如果在所有的最大匹配的方案中都包含了起点 \(S\) ，那么先手必胜，否则先手必败。

证明：

若所有最大匹配方案包括了 \(S\) ，则先手可以走到一个匹配点 \(p_1\) ，每一步后手都会走到一个新匹配点。假设后手走到了未匹配点 \(p_n\) ，考虑当前所走步：\(S \to p_1 \to p_2 \to ... \to p_{n - 1} \to p_{n}\) ，则 \((p_1, p_2), (p_3, p_4), ... (p_{n - 1}, p_{n})\) 以及其他匹配对构成了不包含 \(S\) 的最大匹配，矛盾。因此后手一定会走到一个匹配点，综上所述，先手一定会选择完最后一个匹配点，后手将无路可走，先手必胜。
若存在一种最大匹配不包含 \(S\) ，则先手每一步只能走到新匹配点，假设先手在某一步走到了非匹配点 \(p_n\) ，则当前路径为 \(S \to p_1 \to p_2 \to ... \to p_{n - 1} \to p_{n}\) ，此时 \((S, p_1), (p_1, p_2), ... , (p_{n - 1}, p_n)\) 加上其他匹配对构成了更大的匹配对数，这与假设矛盾。因此每一步先手后会走到新匹配点，后手走与该点匹配的点即可，最终后手一定会选择完最后一个匹配点，先手将无路可走，后手必胜。

如何确定某个点 \(S\) 在最大匹配中不可或缺呢？

考虑先求该二分图的最大匹配，然后删除 \(S\) 点，再算一次最大匹配，若二者相等说明 \(S\) 不是最大匹配中不可或缺的点，反之这说明所有的最大匹配方案中都有 \(S\) 。

数据结构与算法

#DFS #二分匹配 #匈牙利算法 #二分图博弈

二分匹配问题 —— 匈牙利算法

https://goer17.github.io/2023/02/25/二分匹配算法详解/

作者

Captain_Lee

发布于

2023年2月25日

许可协议

记忆化 DFS 上一篇

LLDB 快速入门下一篇